Récursivité

Sources

visualgo.net
u-picardie aller fouiller un peu, ça semble bien !
wikipedia.org
stackoverflow

Codes

Repo

Résumé

Résumé cp3

Definition

Un objet est dit récursif si il se définit à partir de lui-même, si il apparait dans sa définition.
Une construction est récursive si elle se définit à partir d’elle-même.

triangle de Sierpinski

Quelques acronymes récursifs courants:

PHP, GNU, LAME, WINE, YAML

En informatique

En informatique, un programme est dit récursif s’il s’appelle lui même. Il s’agit donc forcément d’une fonction.

Exemple: $\large factorielle:\quad $ $ n! = 1 \cdot 2 \cdot \ldots \cdot n \Rightarrow n! = n \cdot (n-1)! $

L’appel récursif est traité comme n’importe quel appel de fonction.

Condition d’arrêt

Pusqu’une fonction récursive s’appelle elle-même, il est impératif qu’on prévoit une condition d’arrêt à la récursion, sinon le programme ne s’arrête jamais !
On doit toujours tester en premier la condition d’arrêt, et ensuite, si la condition n’est pas vérifiée, lancer un appel récursif.

Exemple de la factorielle: $ si $ $ n \neq 1, \quad n \cdot (n-1)! $ $ sinon$$, \quad n! =1 $

main()

animation

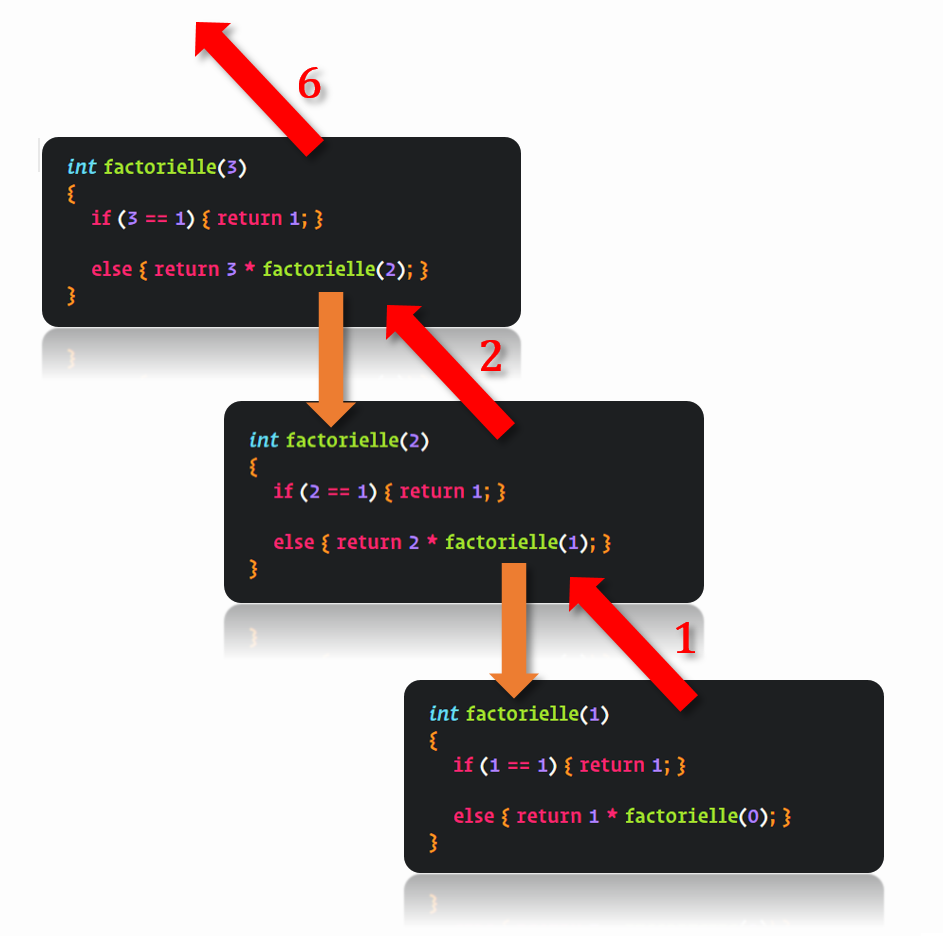
Pile d’execution (stack)

La récursivité fonctionne car chaque appel de fonction est différent. L’appel d’une fonction se fait dans un contexte d’execution propre, qui contient:

l’adresse mémoire de l’instruction qui a appelé la fonction
les valeurs des paramètres et des variables définies par la fonction

version interactive

Prévoir à l’avance le nombre d’appels d’une fonction récursive pouvant être en cours simultanément en mémoire est impossible. La récursivité suppose donc une allocation dynamique de la mémoire (à l’execution).

Attention: éxecuter trop d’appels de fonction fera déborder le stack !

Récursif VS itératif

Il est souvent possible d’écrire un même algorithme en itératif et en récursif.

L’exécution d’une version récursive d’un algorithme est généralement un peu moins rapide que celle de la version itérative, même si le nombre d’instructions est le même (à cause de la gestion des appels de fonction).

Un algorithme récursif peut conduire à exécuter bien plus d’instructions que la version itérative.

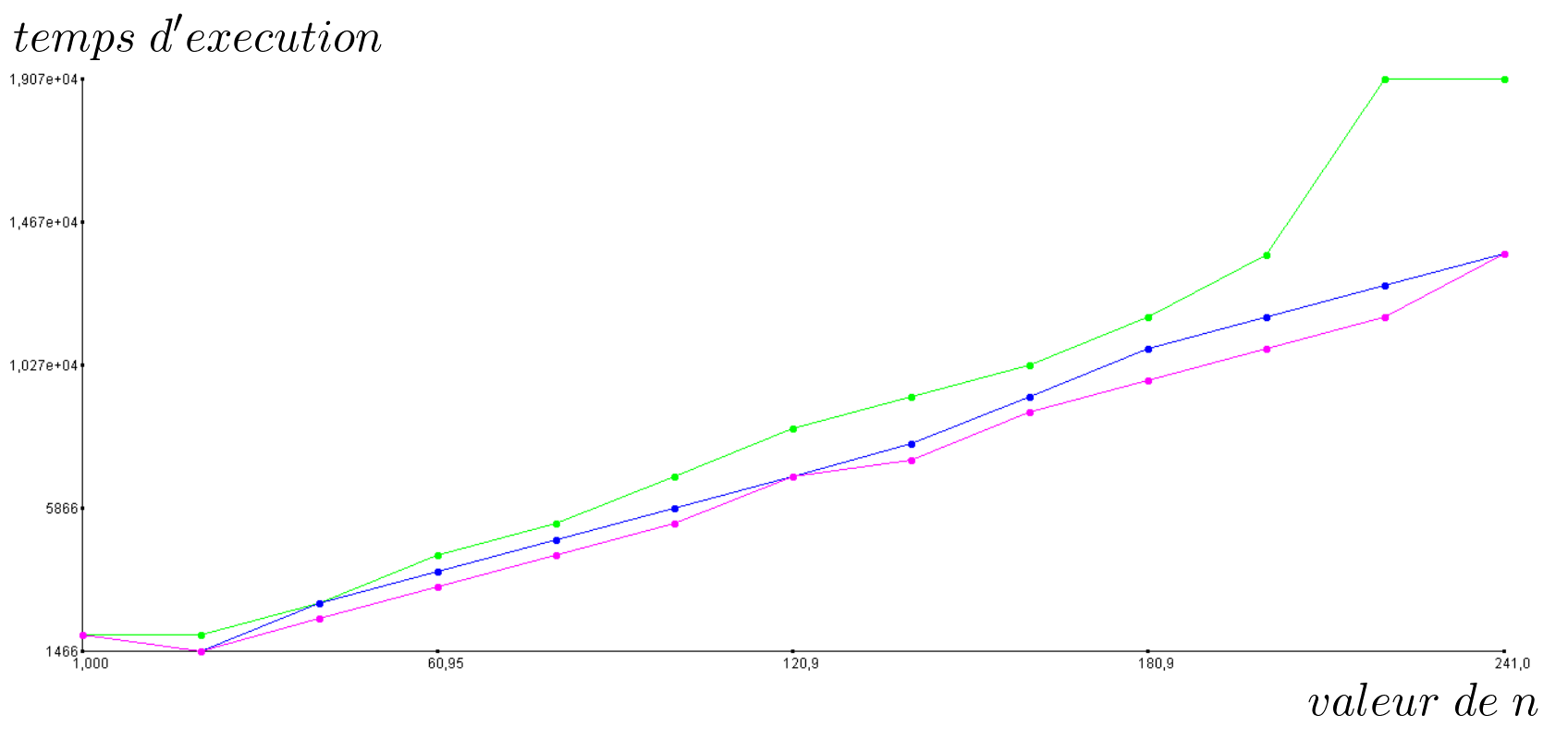
Exemple: la suite de Fibonacci

Suite de Fibbonacci ($ n = 45 $)

Par définition, les deux premiers nombres de la suite de Fibonacci sont 1 et 1 ou 0 et 1. Nous devons en tenir compte pour l’implémentation.

récursif:

int fib1(int n) {
    if (n == 0)
    {
        return 0;
    }
    else if (n == 1)
    {
        return 1;
    }
    return fib1(n-1) + fib1(n-2);
}

// output:
// 1134903170
// 10.859 seconds

Temps d’execution: $ \color{red}{10.859} \; secondes $

version plus compacte:

int fib2(int n) 
{
    if (n < 2)
    {
     return n;
    }     
    return (fib2 (n - 1) + fib2 (n - 2));
}

// output:
// 1134903170
// 10.738 seconds

Temps d’execution: $ \color{red}{10.738} \; secondes $

version très compacte:

 int fib3(int n) { return (n < 2)? n: fib3(n-1)+fib3(n-2); }

// output:
// 1134903170
// 9.752 seconds

Temps d’execution: $ \color{red}{9.752} \; secondes $

itératif:

int fib_it(int n)
{
    int a = 1; 
    int b = 1;
    for (int i = 3; i <= n; i++) {
        int c = a + b;
        a = b;
        b = c;
    }           
    return b;
}

// output:
// 1134903170
// 0.389 seconds

Temps d’execution: $ \color{green}{0.389} \; secondes $

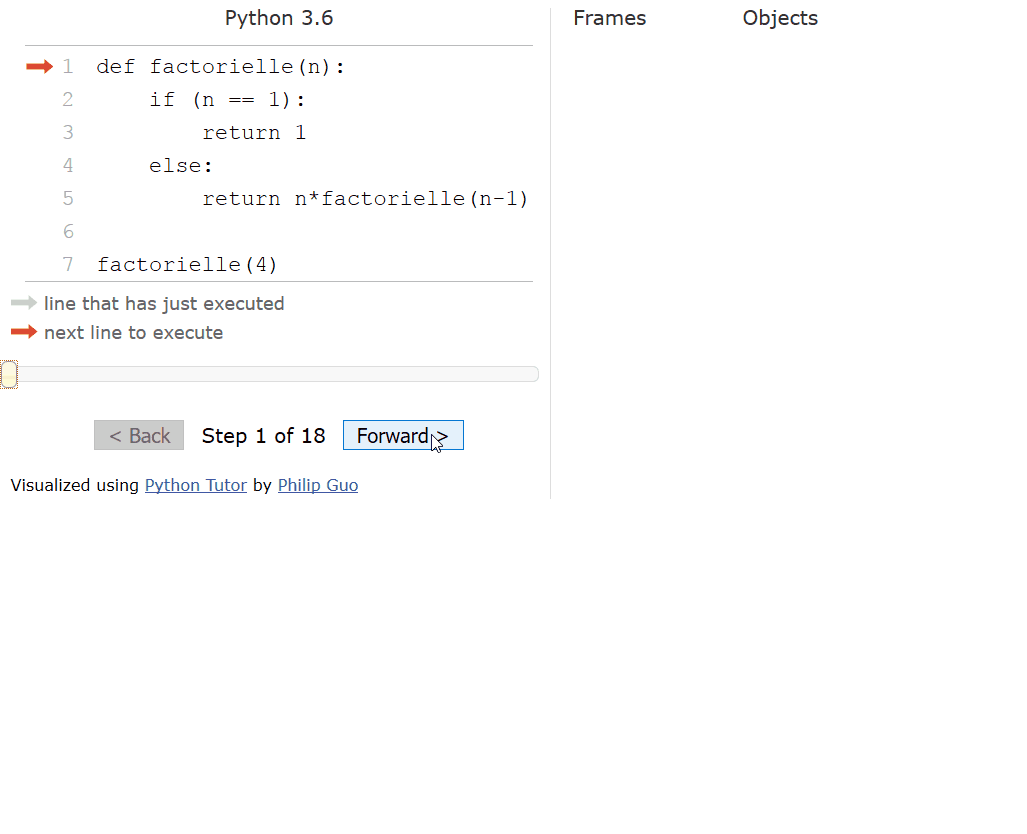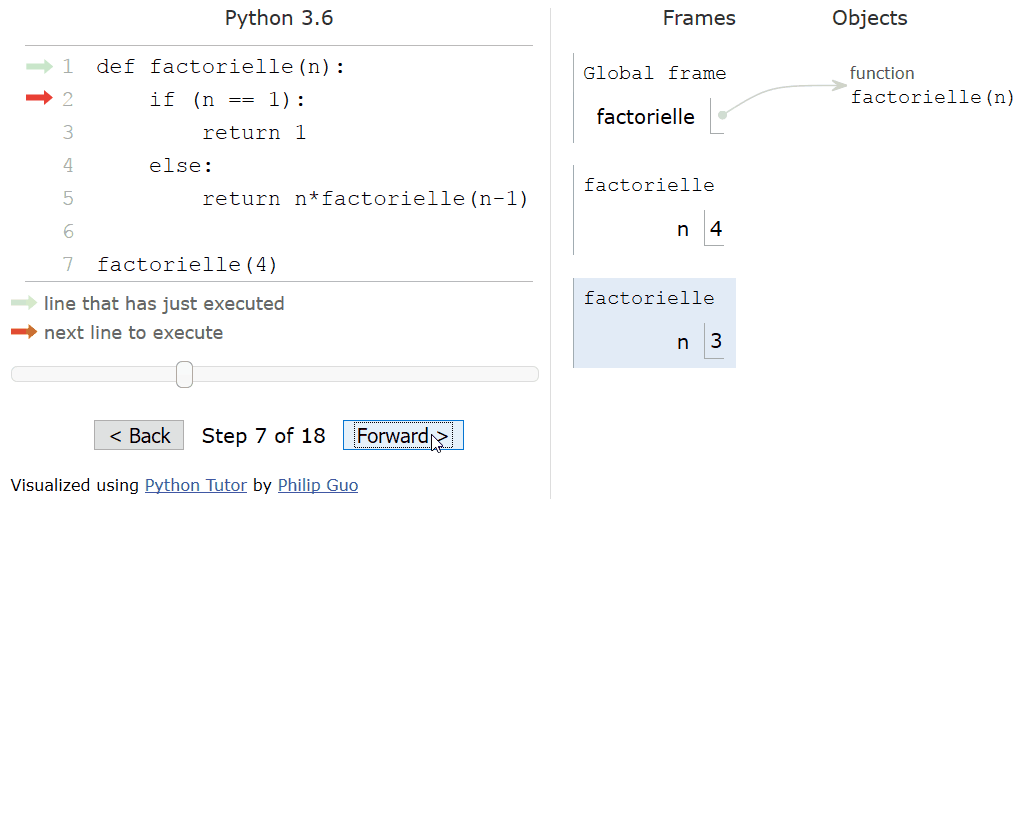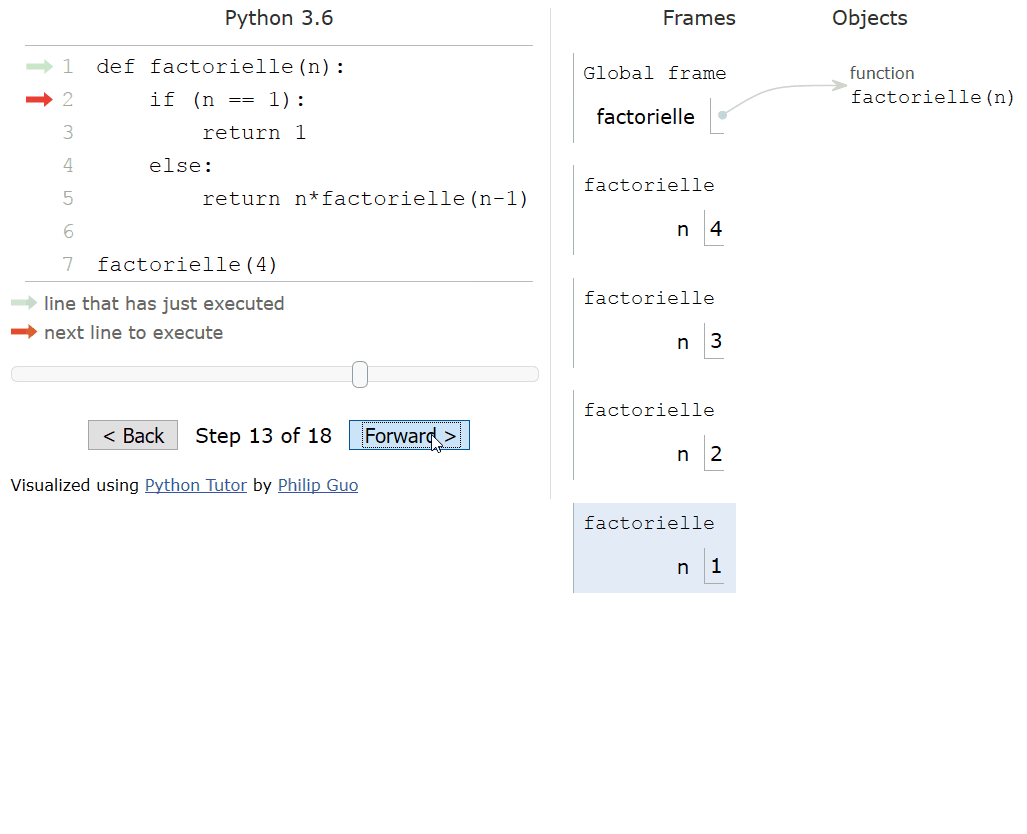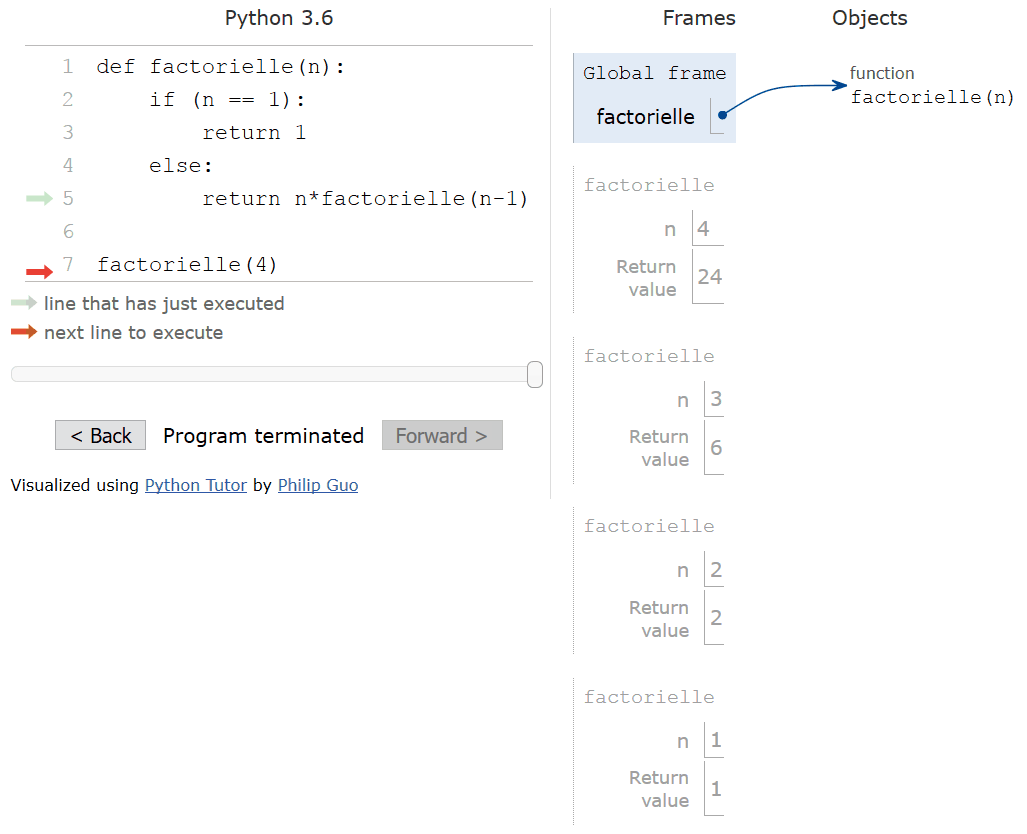
Les différences de temps d’éxecution parlent pour elles mêmes et cette animation nous aide à en comprendre la raison:

Récursivité terminale et non terminale

En programmation, on distingue, pour des raisons d’efficacité, 2 types d’algorithmes récursifs.

1. récursivité Terminale

Un algorithme est terminal si aucune opération ne sui l’appel récursif. C’est l’appel récursif qui “termine” l’algorithme. Toutes les opération sont faites avant l’appel récursif: La phase de remontée devient alors inutile (elle ne fait aucun traitement, hormis le réajustement de la pile). La récursivité terminale revient à appliquer l’adage Diviser pour régner de la façon suivante:

On traite la données courante
Le même traitement est appliqué au reste des données

2. Récursivité non- terminale

Un algorithme récursif est non-terminal lorsque des opérations suivent l’appel récursif. C’est notament le cas lorsque l’appel récursif est utilisé dans une expression pour calculer un résultat. Toutes les opérations ne sont pas faites avant l’appel récursif: la phase de remontée fait une partie du traitement, elle contient souvent la majorité des opérations. La récursivité no-terminale revient à appliquer l’adage diviser pour régner de la façon suivante:

On réduit le problème à son cas trivial
On traite le cas et on élargit l’ensemble des données traitées.

Points cruciaux pour la programmation récursive

Avoir une condition terminale
Avoir un appel récursif dont un des paramètres converge vers la condition terminale
S’assurer que la condition est TOUJOURS atteinte après un nombre fini d’appels

Quand éviter d’utiliser un algorithme récursif ?

Lorsque la récurence est d’ordre plus grande que 1 (c’est à dire que l valeur au rang $ n $ ne dépend pas seulement du rang $ n-1 $, mais aussi de $ n-2 $, voir $ n-3 $,… )
Une utilisation “aveugle” de la récursivité impliquera une redondance de calculs. Dans ce cas, il peut être utile de dérouler l’algorithme avant de l’implémenter pour s’assurer qu’il ne génère pas d’opeerations inutiles.

Récursivité et itérations

Tout algorithme récursif a un équivalent itératif. La réciproque est également vraie en théorie, mais le passage de l’un à l’autre n’est pas toujours aisé. La procédure de derécursivation consiste à gérer dans le programme le comportement de la pile lors des appels récursifs.

En règle générale, un algorithme récursif est moins performant qu’un algorithme itératif : Chaque appel récursif nécessite d’empiler le contexte de la fonction (cadre de pile), puis la condition terminale atteinte, dépiler ce contexte avant d’exécuter les instructions qui suivent l’appel récursif. La création, le changement et la libération de contextes sont donc des opérations supplémentaires non réalisées par l’équivalent itératif. Les algorithmes récursifs sont donc moins performants que leurs équivalents itératifs.

Exception à cette règle, la récursivité terminale est détectée par la majorité des compilateurs et comme il n’y pas d’instruction à exécuter après l’appel récursif terminal, la phase de remontée pourra être supprimée. Dans la plupart des cas, une fonction récursive terminale aura donc la même performance que son équivalente itérative. La récursivité sera alors privilégiée, pour sa lisibilité et son élégance.

Précisions sur les deux types de récursivité (terminal/non terminal)

Une fonction récursive est dite terminale si aucun traitement n’est effectué à la remontée d’ un appel récursif (sauf le retour d’une valeur).
Une fonction récursive est dite non terminale si le résultat de l’appel récursif est utilisé pour réaliser un traitement (en plus du retour d’une valeur).

Exemple de non terminalité : forme récursive non terminale de la factorielle, les calculs se font à la remontée. C’est l’exemple au détbut de cette page !

fonction avec retour entier factorielleNT(entier n)
debut
    si (n = 1) alors
        retourne 1;
    sinon 
        retourne n*factorielleNT(n-1);
    finsi
fin

Exemple de terminalité :

On peut facilement rendre notre fonction factorielle terminale:

// la fonction doit être appelée en mettant resultat à 1

 fonction avec retour entier factorielleT(entier n, entier resultat)
 debut
    si (n =1) alors
        retourne resultat;
    sinon
        retourne factorielleT(n-1, n * resultat);
    finsi
fin

Intérêt de la récursivité terminale

Une fonction récursive terminale est en théorie plus efficace (mais souvent moins facile à écrire) que son équivalent non terminale: il n’y a qu’une phase de descente et pas de phase de remontée.

En récursivité terminale , les appels récursifs n’ont pas besoin d’êtres empilés dans la pile d’exécution car l’appel suivant remplace simplement l’appel précédent dans le contexte d’exécution.

Certains langages utilisent cette propriété pour exécuter les récursions terminales aussi efficacement que les itérations.

Il est possible de transformer de façon simple une fonction récursive terminale en une fonction itérative : c’est la dérécursivation.

Une fonction récursive terminale a pour forme générale:

fonction avec retour T recursive(P)
debut
    I0
    si (C) alors
        I1
    sinon
        I2
        recursive(f(P));
    finsi
fin    

T est le type de retour
P est la liste des paramètres
C est la condition d’arrêt
I0 le bloc d’instructions exécuté dans tous les cas
I1 le bloc d’instructions exécuté si C est vraie
I2 est le bloc d’instructions exécuté si C est fausse
f la fonction de transformation des paramètres

Fonction itérative correspondante:

fonction avec retour T iterative(P)
debut
    IO
    tantque (non C) faire
        I2
        P <- f(p);
        I0;
    fintantque
    I1

Dérécursivation de la factorielle terminale:

// cette fonction doit être appelée avec a=1
fonction avec retour entier factorielleRecurTerm(entier n, entier a)
debut
    si (n <= 1) alors
        retourne a;
    sinon
        retourne factorielle(n-1,n*a);
    finsi
fin

fonction avec retour entier factorielleIter(entier n, entier a)
debut
    tantque (n > 1) faire
        a <– n*a;
        n <– n-1;
    fintantque
    retourne a;
fin

Forme générale d’une fonction récursive non terminale:

fonction avec retour T recursive(P)
debut
    I0
        si (C) alors
            I1
        sinon
            I2 
            recursive(f(P));
            I3
    finsi
fin

T est le type de retour P est la liste des paramètres C est la condition d’arrêt I0 le bloc d’instructions exécuté dans tous les cas I1 le bloc d’instructions exécuté si C est vraie I2 et I3 les blocs d’instructions exécutés si C est fausse f la fonction de tranformation des paramètres

La fonction itérative correspondante doit gérer la sauvegarde des contextes d’exécution (valeurs des paramètres de la fonction).

La fonction itérative correspondante est donc moins efficace qu’une fonction écrite directement en itératif.

Exemples d’algorithmes récursifs

Factorielle

Retourne la factorielle d’un nombre ($ !n $)

int facto(int n) {
    if (n == 1) { return 1;}
    return facto(n-1)*n;  
}

Récursion non-terminale

Descending

Print les nombres à partir de n $ jusque $ 0 $

void descending(int n) {
    if (n < 0) { return; }
    cout << n << " ";
    descending(n-1);
}

Récursion terminale

Ascending

Même chose que le précédent mais de $ 0 $ à $ n $

void ascending(int n) {
    if (n < 0) { return; }
    ascending(n-1);
    cout << n << " ";
}

Récursion terminale. Comparer avec le précédent

Somme

Retourne la somme des nombres de $ 1 $ à $ n $

int somme(int n) {
    if (n == 0){ return n; }
    return somme(n-1) + n;
}

Récursion non-terminale

SommeTab

Retourne la somme des nombres dans un tableau

int sommeTab(int *t, int len) {
    if (len == 0) { return t[len]; }
    return t[len] + sommeTab(t, len-1);
}

Récursion non-terminale

multiple de 13

bool multiple13(int n) {
    if (n == 13) { return true; }
    if (n < 13)  { return false; }
    multiple13(n-13);
}

Récursion terminale

Elever à la puissance (NT)

Élève $a$ à la puissance $n$ss

int puissance(int a, int n) {
    if (n == 0) { return 1; }
    return puissanceNT(a, n-1)*a;
}

Récursion non-terminale

Elever à la puissance (T)

Élève $a$ à la puissance $n$ss

int puissanceT(int a, int n, int t=1) {
    if (n == 0) { return t; }
    t *= a;  
    puissanceT(a, n-1, t);
}

Récursion terminale

Palindrome

bool palindrome(string s, int g, int d) {
    if ((d-g)/2 == 0) { return true; }
    if (s[g] == s[d]) { palindrome(s, g+1, d-1); }
    else { return false; }
}

Récursion terminale

Cherche valeur

bool searchVal(int *t, int g, int d, int &idx, int val) {
    if (g > d) { 
        return false; 
    }
    if (t[g] == val) {
        idx = g;
        return true;
    }
    return searchVal(t,g+1,d,idx,val);
}

Récursion terminale

Fibbonacci (c’est mal !)

int fib(int n) {
      return (n < 2)? n: fib(n-1)+fib(n-2);
}

Algorithmes de tri en mode récursif

Tri-bulle

void echange(int *t, int idx) {
    int temp = t[idx];
    t[idx]   = t[idx-1];
    t[idx-1] = temp;
}

void triBulle(int *t, int g, int d) {
    if (d-g >= 1) {
        for (int i = d; i >= g; --i) {
            if (t[i] < t[i-1]) {
                echange(t, i);
            }
        }
        triBulle(t, g+1, d);
    }
}

Récursion terminale

Tri-extract

void echanger(int *t, int a, int b)
{
    int temp = t[a];
    t[a] = t[b];
    t[b] = temp;
}

void placerMinGauche(int *t, int g, int d) {
    int idxMin  = g;
    for (int i = g+1; i <= d; ++i) {
        if (t[i] < t[idxMin]) {
            idxMin = i;
        }
    }
    echanger(t, g, idxMin);
}

void triExtract(int *t, int g, int d) {
    if (d-g >= 1) {
        placerMinGauche(t,g,d);
        triExtract(t,g+1,d);
    }
}

Récursion terminale

Tri-insert

void insertion(int *t, int g, int idx) {
    int j = idx-1;
    int temp = t[idx];
    while ((t[j] > temp) && (j >= g)) {
        t[j+1] = t[j];
        j--;
    }
    t[j+1] = temp;
}

void triInsert(int *t, int g, int d) {
    if (d - g >= 1) {
        triInsert(t,g,d-1);
        insertion(t,g,d);
    }
}

Récursion terminale

Résumé

Résumé cp3

Directory

Récursivité

Sources

Codes

Résumé

Definition

En informatique

Condition d’arrêt

Pile d’execution (stack)

Récursif VS itératif

Suite de Fibbonacci ($ n = 45 $)

récursif:

itératif:

Récursivité terminale et non terminale

1. récursivité Terminale

2. Récursivité non- terminale

Points cruciaux pour la programmation récursive

Quand éviter d’utiliser un algorithme récursif ?

Récursivité et itérations

Précisions sur les deux types de récursivité (terminal/non terminal)

Exemple de terminalité :

Intérêt de la récursivité terminale

Une fonction récursive terminale a pour forme générale:

Fonction itérative correspondante:

Dérécursivation de la factorielle terminale:

Forme générale d’une fonction récursive non terminale:

Exemples d’algorithmes récursifs

Factorielle

Descending

Ascending

Somme

SommeTab

multiple de 13

Elever à la puissance (NT)

Elever à la puissance (T)

Palindrome

Cherche valeur

Fibbonacci (c’est mal !)

Algorithmes de tri en mode récursif

Tri-bulle

Tri-extract

Tri-insert

Résumé