Algorithmes de tri
Directory
Liens
1 Tri-Bulle (Bubble-sort)
Simple
-
Tous les parcours commencent à la fin du tableau
n-1. -
Lors de chaque parcours, l’élément actuelement pointé par la variable d’itération
j, si il est plus petit que l’élément à sa gauchej-1est échangé avec ce dernier.

void echange(int *t, int idx)
{
int temp = t[idx];
t[idx] = t[idx-1];
t[idx-1] = temp;
}
-
Si l’élément à sa gauche
j-1est plus petit, il n’y a pas d’échange. -
L’élément le plus petit se retrouve au début du tableau à la fin du premier parcours.
-
Tant que l’élément pointé par la variable d’itération est plus petit que
j-1, il se déplace vers le début du tableau. -
Au second parcours, le second élément le plus petit se retrouvera trié à droite de l’élément le plus petit et ainsi de suite jusqu’au tri complet du tableau.
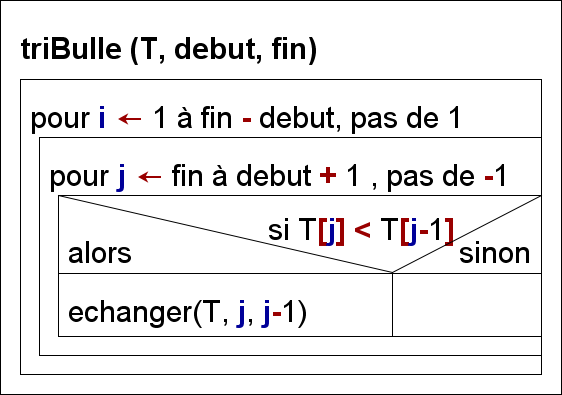
void triBulle(int *t, int g, int d)
{
for (int i = 1; i <= d-g; i++)
{
for (int j = d; j >= g+1; j--)
{
if (t[j] < t[j-1]) { echange(t,j); }
}
}
}
Complexité
La boucle extérieur qui est responsable du nombre
de parcours du tableau a sa variable d’itération qui est égale au nombre de cases du tableau -1.
La boucle intérieur qui est responsable du nombre de comparaisons par parcours a sa variable d’itération
que est également égale au nombre de cases du tableau -1.
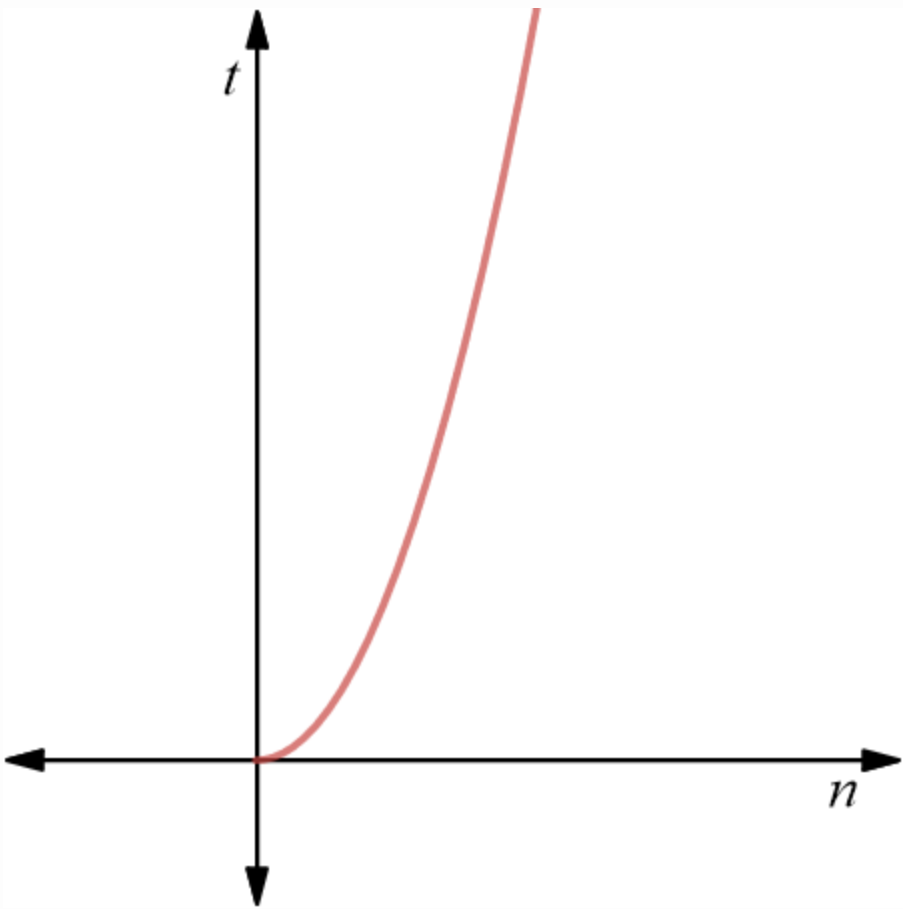
$ (n-1) \cdot (n-1)^2 $ comparaisons La complexité de cet version de l’algorithme est de:
Itératif
Nous pouvons dire qu’après i parcours du tableau, les i plus petits éléments seront triés. Il n’est donc plus nécéssaire que les parcours itèrent sur ces cases ce qui suggère une première amélioration:
void triBulle(int tab[], int debut, int fin)
{
for (int i = 1; i <= fin; i++)
{
for (int j = fin; j >= debut+i; j--)
{
display(tab, i, j, 8);
if (tab[j] < tab[j-1])
{
swap(tab, j, j-1);
}
}
}
}
Plusieurs éléments peuvent remonter lors d’un même parcours. Avant que l’élément le plus petit restant ne remonte jusqu’à sa place définitive, tous les éléments qui ont à leur gauche (j-1) un élément plus petit remontent au moins d’une case.
Flag
Le tableau est donc suceptible d’être trié avant les $N-1$ parcours. Il serait donc profitable de cesser les parcours dés que le tableau est trié surtout dans le cas d’un tableau qui est totalement trié dés le début. C’est ce que nous permet la prochaine amélioration qui stop la fonction si un parcours entier a été fait sans aucun échange:
void triBulle(int *t, int g, int d)
{
int j = 1;
bool flag = true;
while (flag)
{
flag = false;
for (int i = d; i >= g+j; i--)
{
if (t[i] < t[i-1])
{
echange(t,i);
flag = true;
}
}
j++;
}
}
Complexité
Le nombre maximum d’échanges reste le même: $\frac{n(n-1)}{2}$
Mais la complexité de l’algorithme a augmenté, ainsi que sa durée d’execution. Cette version n’est donc interessante que pour des tableaux très proche d’un tableau ordonné dés le début.

Étude de la stabilité
Si deux éléments d’indice i et j avec i < j.
tout élément de clé strictement inférieur se
placera à leur gauche. Ils se trouveront donc
dans des cases d’indice k et k+1. Lors de la
comparaison des clés des ces deux éléments,
ils ne seront donc pas échangés et donc l’ordre
de leurs emplacements d’origine est respecté.
L’élément d’indice i se trouvera dans la case
k et celui d’indice j > i dans la case d’indice
k + 1. La métode est donc stable.
Cet algorithme possède une assymétrie particulière: Un seul élément de petite clé mal classé du côté des éléments de grande clé, d’un tableau presque trié prend sa place (début) après un seul parcours du tableau. Par contre un élément de grande clé, mal classé du coté des petites clés descend (vers la fin) à sa place à raison d’une case par parcours. Le tableau suivant:
[12] [18] [42] [44] [55] [67] [94] [6]
Debut Fin
…est trié en deux parcours en utilisant la fonction triBulle itératif + flag. Un parcours pour faire monter (vers le début) le clé 6 dans sa case définitive et un autre parcours pour constater que le tableau est trié. Le tableau suivant quant à lui…
[94] [6] [12] [18] [42] [44] [55] [67]
Debut Fin
… nécessite sept parcours pour obtenir un tri complet: Les sept valeurs de clé plus petites montent à leur place à raison d’une case par parcours.
Cette asymétrie suggère une troisième amélioration de l’algorithme. Pour compenser l’asymétrie décrite, le sens de deux parcours consécutifs du tableau est alterné.
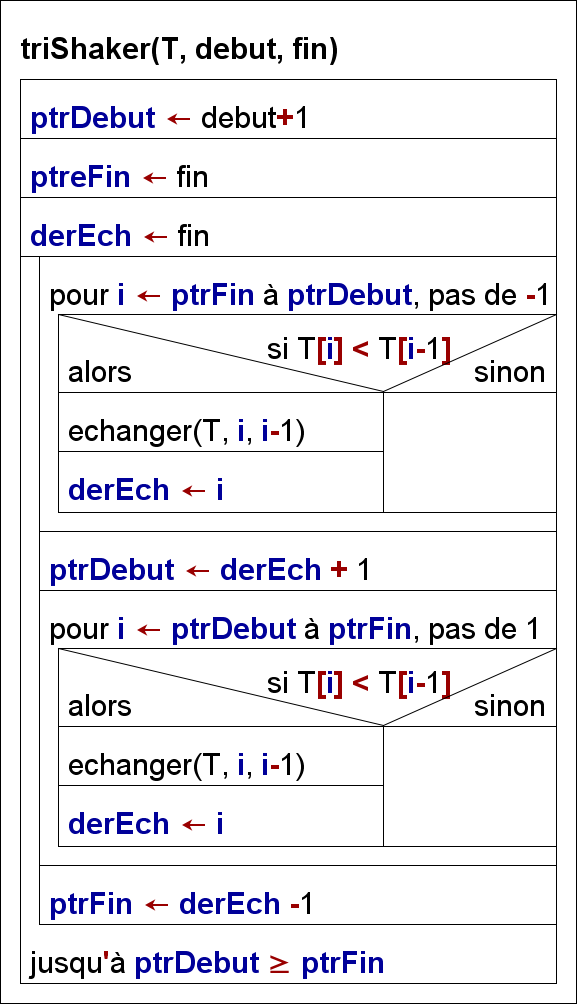
2 Tri-Shaker
Pour compenser l’asymétrie décrite, le sens de deux parcours consécutifs du tableau est alterné.
void swap(int tab[], int a, int b)
{
int temp = tab[a];
tab[a] = tab[b];
tab[b] = temp;
}
void triShaker(int tab[], int g, int d)
{
int ptrG = g+1;
int ptrD = d;
int derEch = d;
cout << "derEch start: " << derEch << endl;
while (ptrG <= ptrD)
{
cout << "ptrG: " << ptrG
<< "\tptrD: " << ptrD
<< "\tderEch: " << derEch
<< endl;
for (int i = ptrD; i >= ptrG; i--)
{
if (tab[i] < tab[i-1])
{
swap(tab, i, i-1);
derEch = i;
}
}
cout << "derEch aller: " << derEch << endl;
ptrG = derEch + 1;
for (int i = ptrG; i <= ptrD; i++)
{
if (tab[i] < tab[i-1])
{
swap(tab, i, i-1);
derEch = i;
}
}
ptrD = derEch -1;
cout << "derEch retour: " << derEch << endl;
}
}
A la fin d’un parcours, les “pointeurs” ptrDebut et ptrFin contiennent les niveaux entre lesquels le prochain parcours sera effectué. Ces pointeurs sont maj en tenant compte du niveau du dernier échange derEch effectué lors d’un parcours.
Ce tri prend fin quand les deux variables ptrDebut et ptrFin sont égales.
Conclusion sur les améliorations
Toutes les améliorations n’ont pas modifié le nombre d’échanges à faire (logique) et réduisent uniquement le nombre de comparaisons redondantes. Un échange (permutation) est généralement une opération plus couteuse qu’une comparaison de de clé. Ce qui fait que si on ne concidère que le pire des cas pour évaluer la complexité des différentes améliorations on se retrouve toujours avec du $\color{red}{O(n^2)}$.
3. Tri par extraction (Selection-sort)
A chaque tour, l’algorithme trouve la valeur la plus petite et la place à sa position définitive.
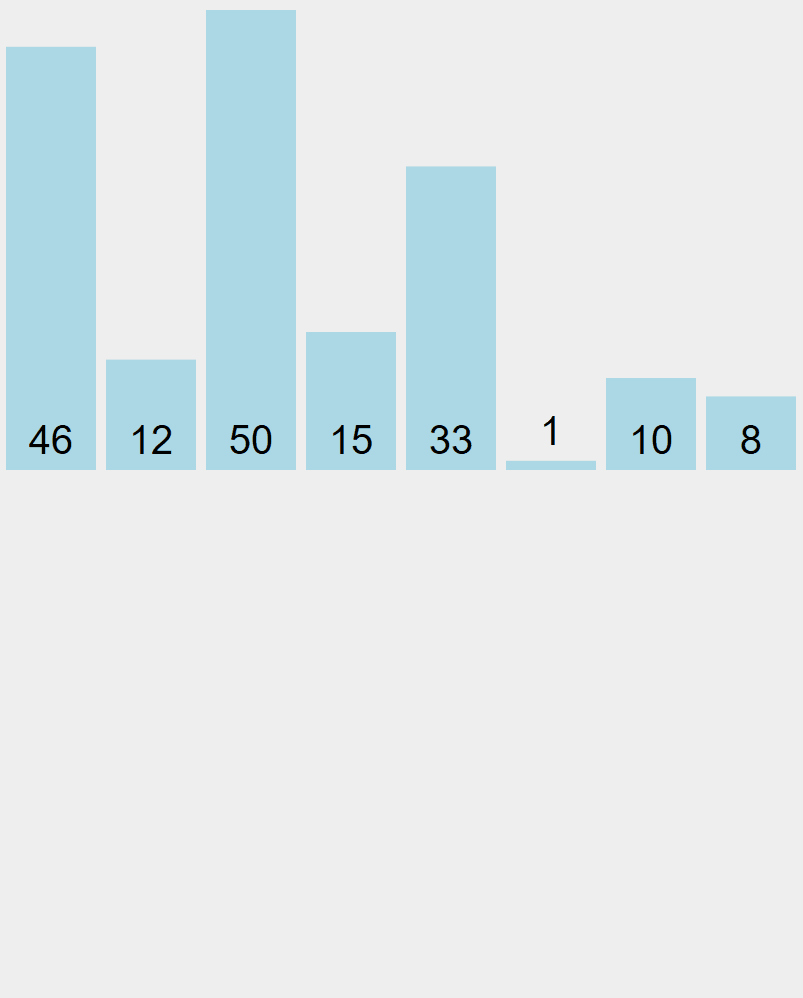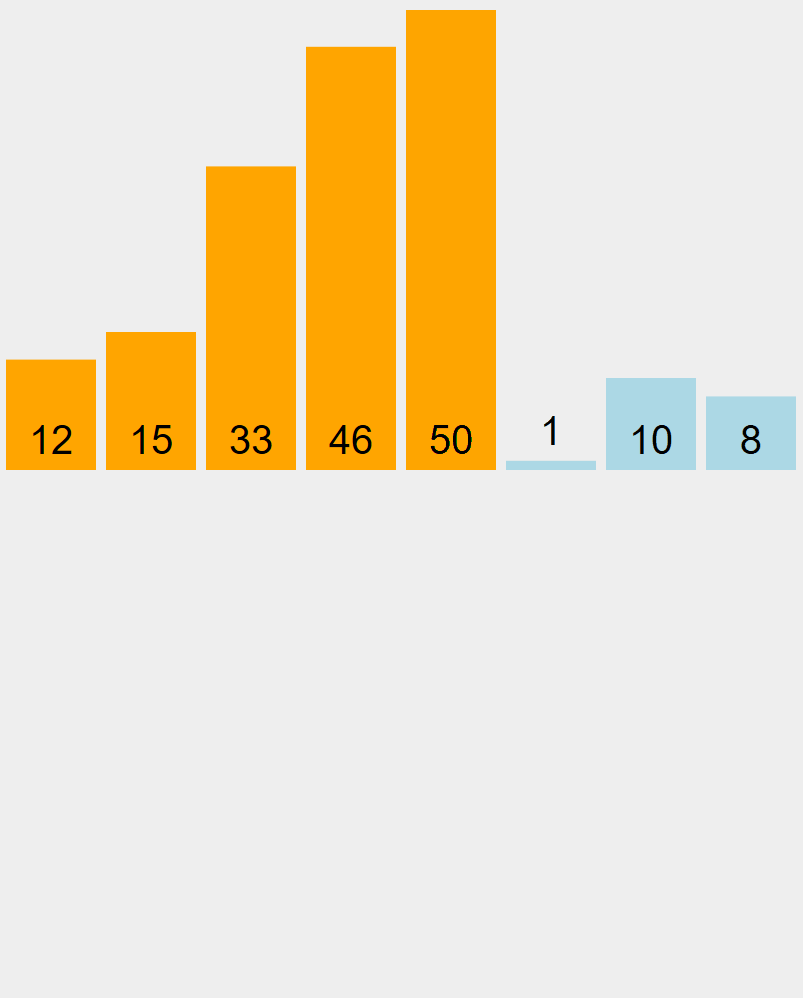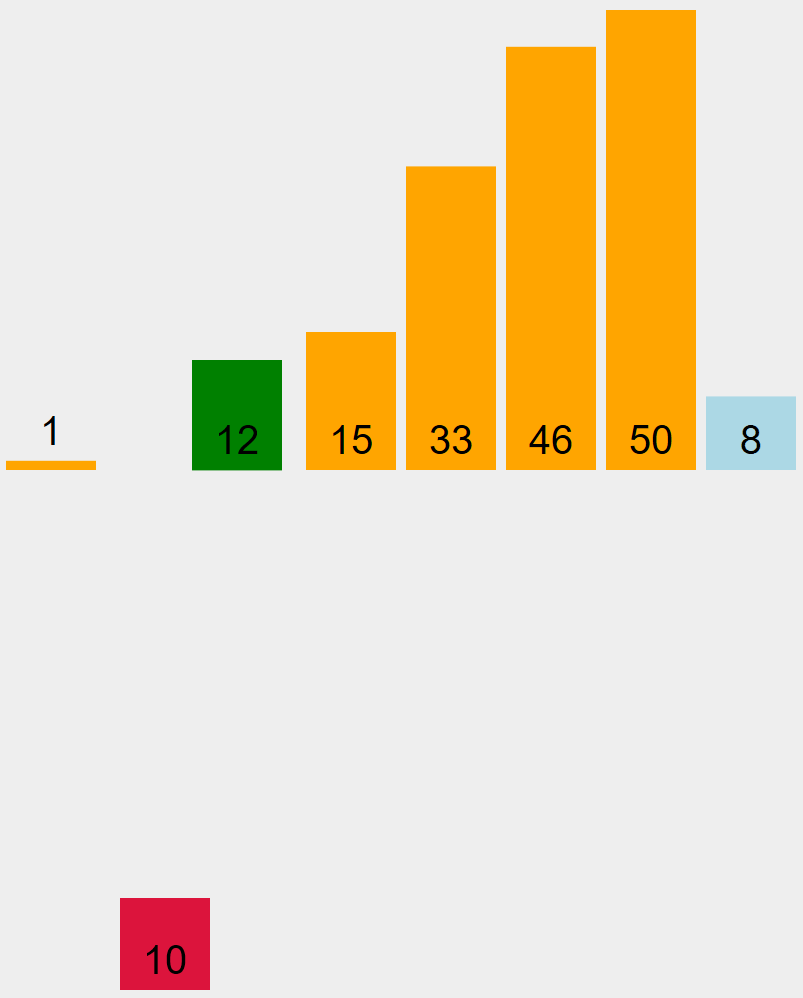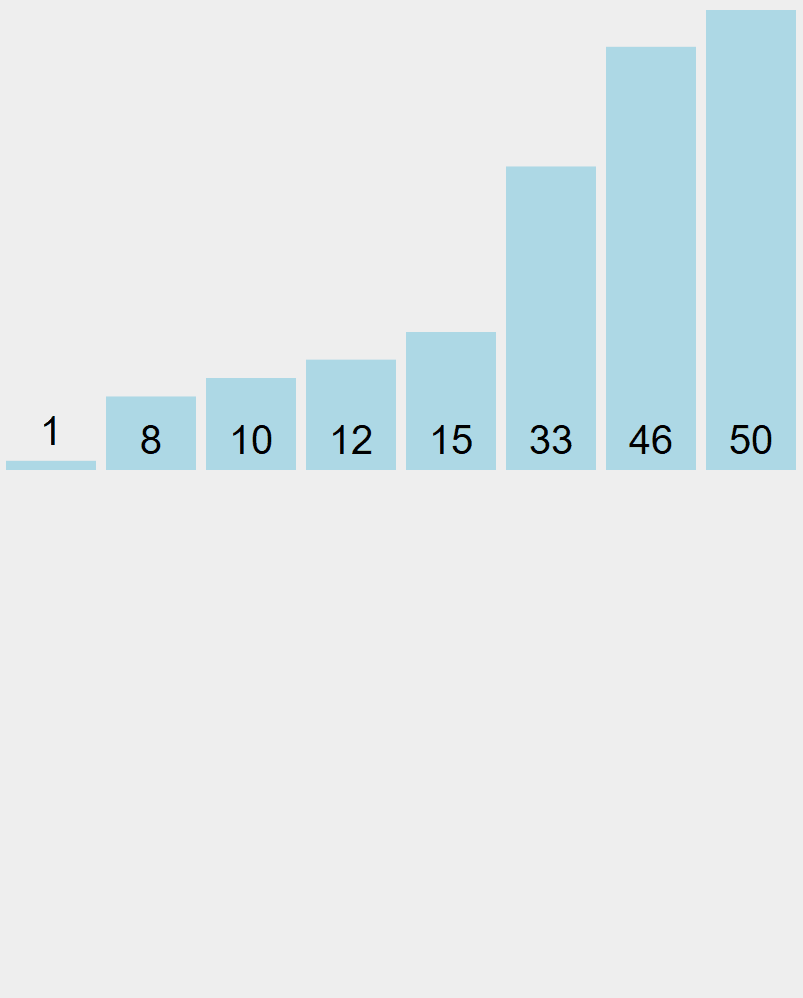
initial
G D
[46] [12] [53] [15] [33] [1] [10] [8]
tour 1
G D
[1] [12] [53] [15] [33] [46] [10] [8]
// valeur la plus petite: 1 change de
// place avec t[G]
G D
[1] [12] [53] [15] [33] [46] [10] [8]
// la premiere case est maintenant definitive
// G se deplace d'une case a droite.
tour 2
G D
[1] [8] [53] [15] [33] [46] [10] [12]
// valeur la plus petite: 8 change
// de place avec t[G]
G D
[1] [8] [53] [15] [33] [46] [10] [12]
// les deux premieres cases sont maintenant
// definitives, G se deplace d'une case vers
// la droite.
Il ne sert à rien d’itérer sur tout le tableau à chaque tour, les valeurs de gauche, une fois placées le sont définitivement. Gauche est incrémenté de 1 à chaque nouveau tour.
On peut donc diviser ce problème en 3 parties distinctes:
- une fonction échange()
- une fonction placerMinimumAGauche()
- triExtraction()

void echanger(int *t, int a, int b)
{
int temp = t[a];
t[a] = t[b];
t[b] = temp;
}

void placerMinGauche(int *t, int g, int d)
{
int idxMin = g;
for (int i = g+1; i <= d; ++i)
{
if (t[i] < t[idxMin])
{
idxMin = i;
}
}
echanger(t, g, idxMin);
}
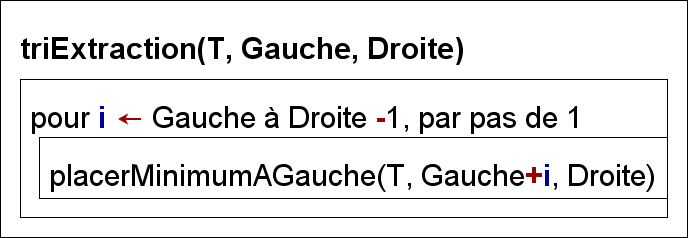
void triExtract(int *t, int g, int d)
{
for (int i = g; i < d; ++i)
{
placerMinGauche(t, g+i, d);
}
}
Lorsque les N-1 éléments ayant les clés les plus petites sont à leur place, le dernier élément qui a la plus grande clé l’est aussi.
Complexité:
L’algorithme placerMinimumAGauche() est exécuté $n-1$ fois pour un tableau de $n$ éléments et ceci indépendamment de l’ordre initial des clés. A chaque exécution, cet algorithme effectue $Droite - Gauche$ comparaisons.
$ n-1 + n-2 + … + 3 + 2 + 1 = \bbox[20px,border:2px solid red] {\frac{(n(n-1))}{2}}$
Le tri par extraction est aussi lent que le tri bulle dans le cas d’un tableau à clés aléatoirement dispersées. Des différences en plus ou en moins peuvent apparaître dans des cas particuliers. Le tri par extraction est innefficace sur un tableau déjà ordonné puisqu’il n’est ps capable de s’en appercevoir.
Stabilité
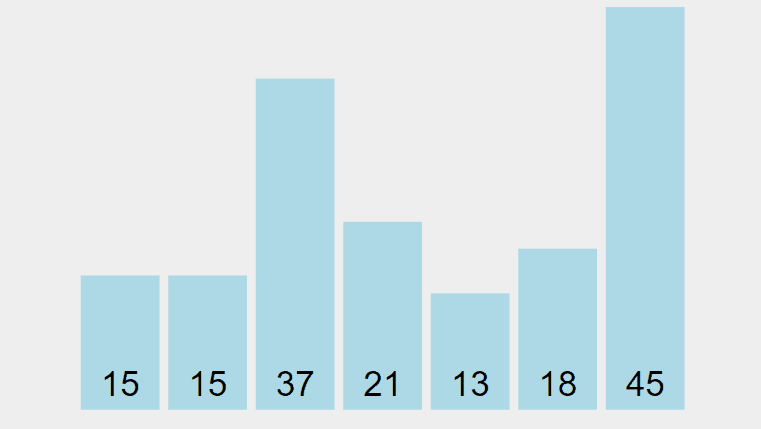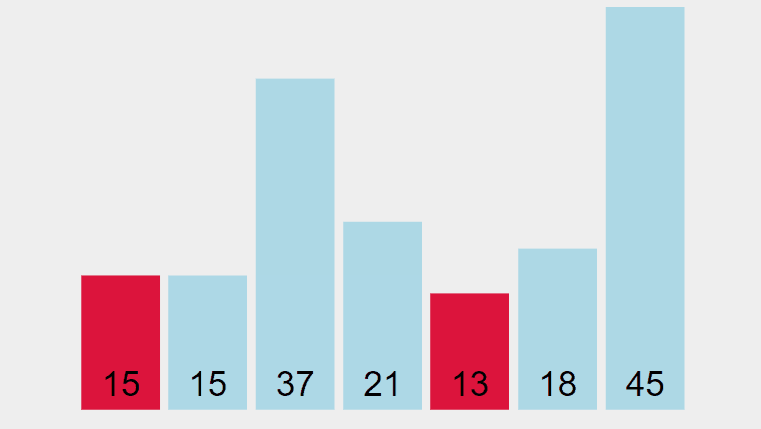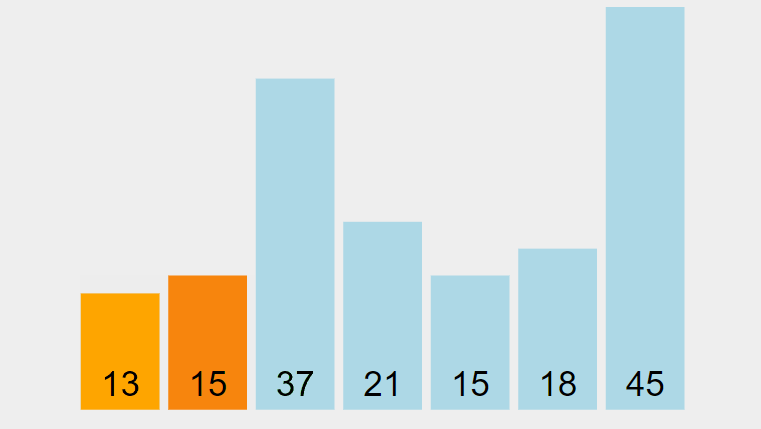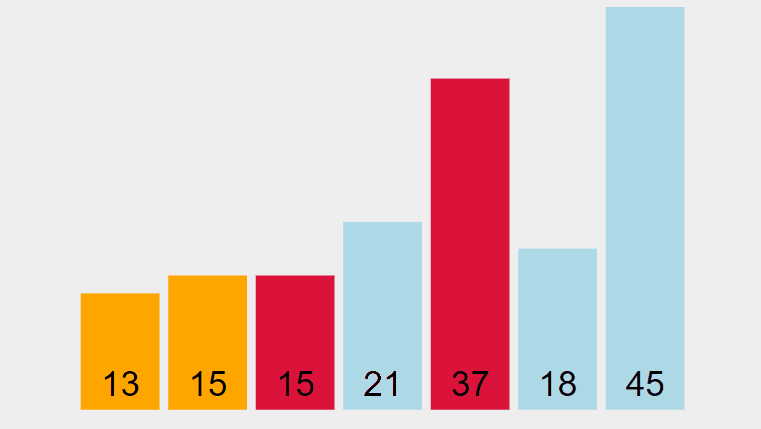
Le tableau suivant comporte deux clés identiques:
[15] [15] [37] [21] [13] [18] [45] // Clé
[ A] [ B] [ C] [ D] [ E] [ F] [ G] // Information
1 2 3 4 5 6 7 // Indice
L’extraction du premier minimum donne:
[13] [15] [37] [21] [15] [18] [45] // Clé
[ E] [ B] [ C] [ D] [ A] [ F] [ G] // Information
1 2 3 4 5 6 7 // Indice
Les deux éléments de même clé 15 ont été échangés l’un par rapport à l’autre. Après exécution de l’algorithme, le tableau ordonné devient:
[13] [15] [15] [18] [21] [37] [45] // Clé
[ E] [ B] [ A] [ F] [ D] [ C] [ G] // Information
1 2 3 4 5 6 7 // Indice
Cet exemple montre que le tri par extraction n’est pas stable.
4. Tri par insertion (Insert Sort)
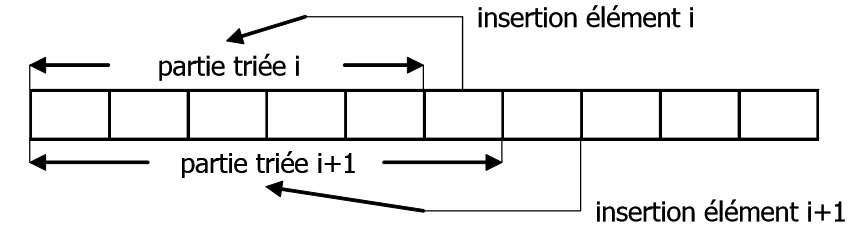
Cette méthode de tri consiste à insérer un élément du tableau qui n’est pas encore à sa place dans une partie déjà ordonnée, puis à recommencer avec les éléments suivant. La première étape montre comment insérer un élément dans la partie déjà triée.
Dans le tableau T suivant, les éléments d’indices $Gauche$ $à$ $i-1$ sont déjà dans l’ordre croissant. L’élément d’indice i doit être inséré.
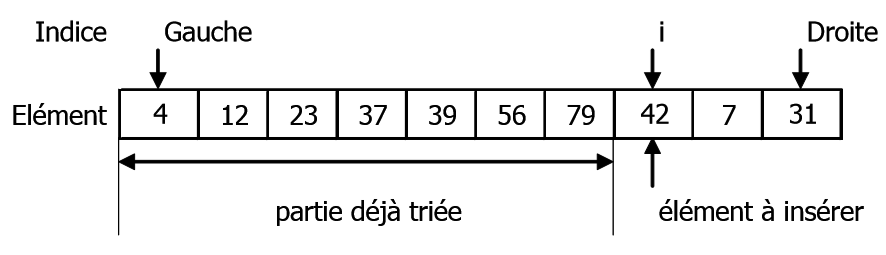
Pour insérer l’élément d’indice i dans la partie du tableau déjà trié, il faut le sauvegarder puis décaler vers la droite tous les éléments dont la clef est supérieure à l’élément à insérer. Ainsi, l’emplacement de l’élément à insérer est trouvé et une case libre est préparée au bon emplacement.
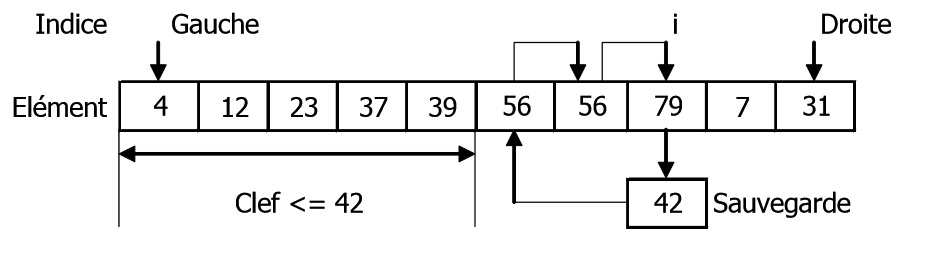
insertion:

A la sortie de la boucle tant que qui permet de reculer en créant une case libre, l’indice j correspond à la case contenant la plus grande clef inférieure ou égale à la clef de l’élément à insérer qui se trouve dans la Sauvegarde (temp).
void insertion(int *t, int g, int idx)
{
int j = idx-1;
int temp = t[idx];
while ((t[j] > temp) && (j >= g))
{
t[j+1] = t[j];
j--;
}
t[j+1] = temp;
}
Pour trier complètement le tableau il suffit d’insérer successivement ses éléments en commençant par le deuxième élément (indice $Gauche+1$) et en terminant par le dernier élément du tableau (indice $Droite$).
void triInsert(int *t, int g, int d)
{
for (int i = g+1; i <= d; ++i)
{
insertion(t,g,i);
}
}
Complexité
La boucle for s’exécute au moins $n-1$ fois et le nombre d’executions de la boucle while dépend du tableau à trier:
-
Dans le meilleur cas, le tableau est déja trié
t[j] > tempest toujours faux et aucun échange de données n’est nécéssaire ce qui fait que la bouclefors’executera $n-1$ fois. La complexité sera donc de $O(n)$ -
Dans le pire cas, le tableau est trié à l’envers et
t[j] > tempest toujours vrai, dans ce cas la bouclewhiles’executera à chaque fois. La complexité sera donc de $ O(n \cdot n) = O(n^2) $

Stabilité
Considérons deux éléments du tableau, ayant la même clef, et d’indices i et j avec $ i < j $. Le parcours de la partie non triée du tableau s’effectuant de $Gauche+1$ vers $Droite$, l’élément d’indice i sera inséré le premier dans la partie déjà triée du tableau, à l’indice i’. Lorsque l’élément d’indice j devra être inséré, il le sera juste après le premier élément qui ne lui est pas strictement supérieur (car l’algorithme décrit ici effectue une comparaison stricte), c’est-à-dire à l’indice $i’+1$. Après le tri, l’élément qui avait pour indice i se retrouve bien avant celui qui avait pour indice j : le tri par insertion est donc stable.
4. Tri par base (radix-sort)
Le principe de ce tri est totalement différent des précédents. Il ne se base pas sur des comparaisons entre les différentes valeurs mais sur un classement successif des valeurs en fonction des chiffres qui la compose en commençant par la valeur des unités, ensuite celle de l’unité des dizaines, puis de l’unité des centaines, … jusqu’au chiffre le plus à gauche.
Pour faire le classement nous avons donc besoin de 10 tableau: un pour chaque chiffre (0 à 9) une fois nos valeurs classées, nous les remettons dans le tableau initial en commançant par les valeurs dans le tableau des 0 en respectant le principe du fifo. Ensuite le tableau des 1, puis des 2 …
Comme le principe du fifo est requis, nous pouvons utiliser des files (queue) à la place de simple tableaux. Cela rend le tout plus simple à gérer, il suffit d’utiliser l’équivalent de la fonction push pour insérer et de pull pour extraire la bonne valeur.
Le nom de ces deux fonctions dépendent de l’implémentation de la file.
Le second parcours fera la même chose mais en classant les nombres par la valeur du chiffre qui représente l’unité des dizaines. Le 3e parcours l’unité des centaines…
Dans les exemples qui suivent, je vais utiliser une classe Queue dont l’imlémentation est spécifiées ici
Le tableau d’éléments à ordonner dans l’ordre croissant de cet exemple contient $n$ éléments et ses indices vont de $Gauche$ à $Droite$ ($0$ à $n-1$)
L’algorithme de tri par base peut facilement être divisé en deux fonctions. Dans un soucis de clarté je vais le diviser en 4 parties qui correspondes aux grandes étapes de l’algorithme.
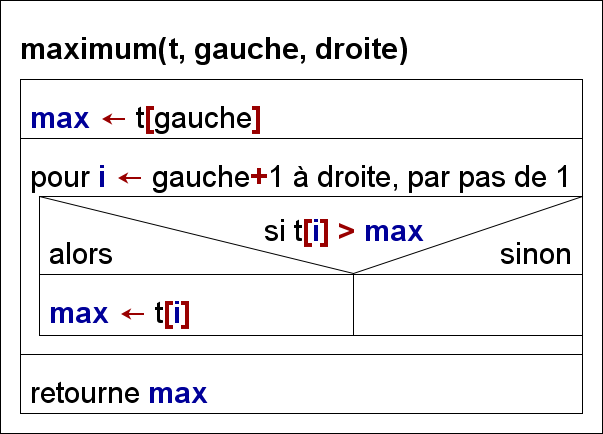
1. fonction maximum
Simple fonction pour itérer sur un tableau et retourner la clé ayant la plus grande valeur.
Nous avons besoin de cette valeur car c’est le nombre de chiffres qui compose le plus grand nombre (ou un autre nombre ayant le même nombre de chiffres) qui va déterminer le nombre de parcours nécéssaire pour trier le tableau.
int maximum(int *t, int g, int d)
{
int max = t[g];
for (int i = g+1; i <= d; ++i)
{
if (t[i] > max)
{
max = t[i];
}
}
return max;
}
2. fonction nombreDeParcours
Nous avons besoin d’une fonction capable de nous retourner le nombre de chiffres qui compose un nombre.
l’entier renvoyé par un cast entier du log en base 10 d’un nombre sera égal au nombre de chiffre qui le compose -1. Nous ajoutons donc +1.

int nbParcours(int *t, int g, int d)
{
return log10(maximum(t,g,d))+1;
}
Le cast est fait automatiquement par le type de la valeur de retour
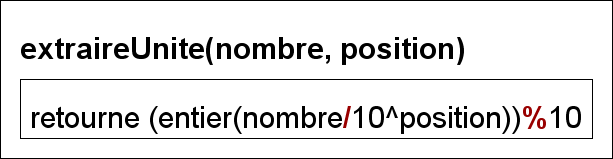
3. fonction extraireUnite
Il nous faut également une fonction capable de retourner une unité spécifique d’un nombre afin de pouvoir faire le classement en fonction de cette dernière.
int extraireUnite(int nb, int pos)
{
return (static_cast<int>(nb/pow(10,pos))%10);
}
Ici, le cast est nécessaire pour éviter l’erreur:
invalid operands of types '__gnu_cxx::__promote_2<int, int, double,
double>::__type {aka double}' and 'int' to binary 'operator%'
return ((nb/pow(10,pos))%10);
^
4 triBase
Après autant de parcours que le nombre de chiffres de la plus grande des clé, le tableau est trié. Cette méthode peut s’appliquer à des clés non numériques (ex : chaines de caractères), pourvu qu’on ait une relation d’ordre entre les symboles utilisés (ex : ordre alphabétique pour une chaîne de caractères).
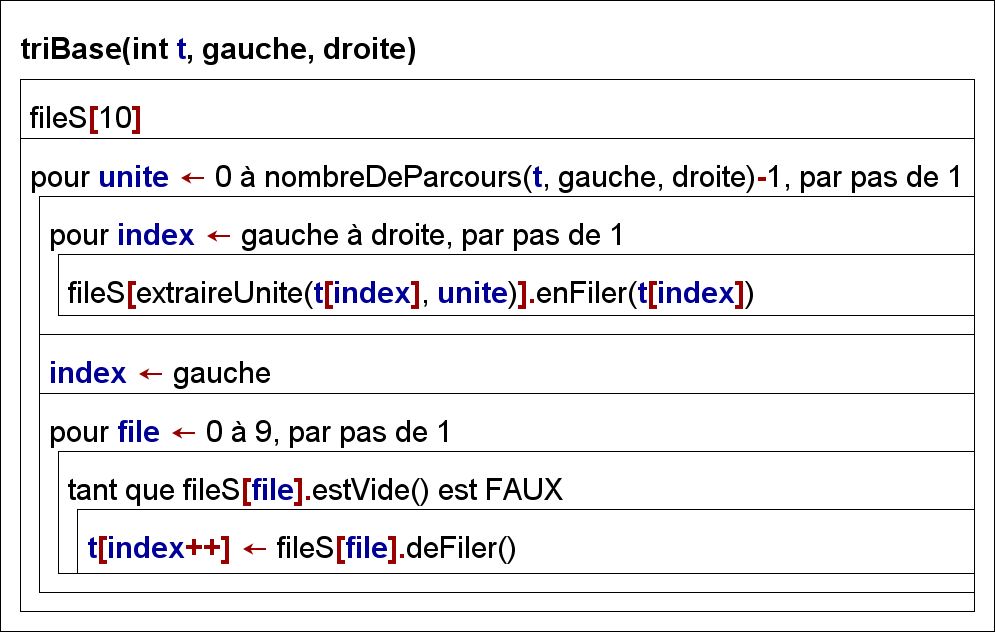
Dans ce structogramme, fileS est un tableau de files permettant d’ordonner t suivant son nième chiffre : fileS[x] contiendra les nombres dont le nième chiffre est x . L’idée est de commencer par distribuer dans ces files les valeurs de t , puis dans un second temps, de mettre à jour le tableau en vidant les files par ordre croissant.
Il y a plusieurs façons de déterminer le nième chiffre d’un nombre. Parmi les plus répandues :
-
Convertir le nombre en chaine de caractère, puis extraire le caractère désiré
-
Arithmétique : $1984 = 1 \cdot 103 + 9 \cdot 102 + 8 \cdot 101 + 4 \cdot 100$ on peut donc aisément retrouver la valeur de chaque chiffre grâce à des divisions par des puissances de 10 et l’opérateur modulo.
Pour compléter le tri il suffit de faire autant de passes que de nombre de chiffres dans la valeur maximale.
La file que j’utilise est issu la classe générique Queue qui hérite de la classe List (liste chainée) toutes deux détaillées ici.
a. sans gestion de la mémoire
void triBase(int *t, int g, int d)
{
Queue<int> fileS[10];
// tri
for (int unite = 0; unite < nbParcours(t,g,d); ++unite)
{
for (int index = g; index <= d; ++index)
{
fileS[extraireUnite(t[index], unite)].enqueue(t[index]);
}
int index = g;
for (int file = 0; file <= 9; ++file)
{
while (fileS[file].isEmpty() == false)
{
t[index++] = fileS[file].dequeue();
}
}
}
}
b. avec gestion de la mémoire
void triBase(int *t, int g, int d)
{
// initialisation
Queue<int> **fileS = new Queue<int>*[10];
for (int file = 0; file <= 9; ++file)
{
fileS[file] = new Queue<int>;
}
// tri
for (int unite = 0; unite < nbParcours(t,g,d); ++unite)
{
for (int index = g; index <= d; ++index)
{
fileS[extraireUnite(t[index], unite)]->enqueue(t[index]);
}
debug(fileS, unite); // visualisation
int index = g;
for (int file = 0; file <= 9; file++)
{
while (fileS[file]->isEmpty() == false)
{
t[index++] = fileS[file]->dequeue();
}
}
}
// nettoyage
for (int file = 0; file <= 9; ++file)
{
delete fileS[file];
}
delete [] fileS;
}
Complexité
Contrairement aux autres algorithmes de tri simples, le tri par base n’utilise pas de comparaisons : il fait partie des tris par distribution.
C’est la copie des valeurs dans des files qui va permettre le tri, on peut donc décider de choisir la copie d’une valeur (affectation) comme opération élémentaire de cet algorithme.
Pour trier un tableau de taille n on doit effectuer k passes, avec k le nombre de chiffres de la plus grande clé.
Lors de chaque parcours, on va recopier les n valeurs dans les files temporaires fileS[x] (n affectations), puis les recopier dans le tableau initial. On aura donc 2 x n opérations élémentaires.
Pour k passes, la fonction de complexité sera donc: $ f(n)=2kn$ Si k est constant, notre algorithne est donc linéaire:
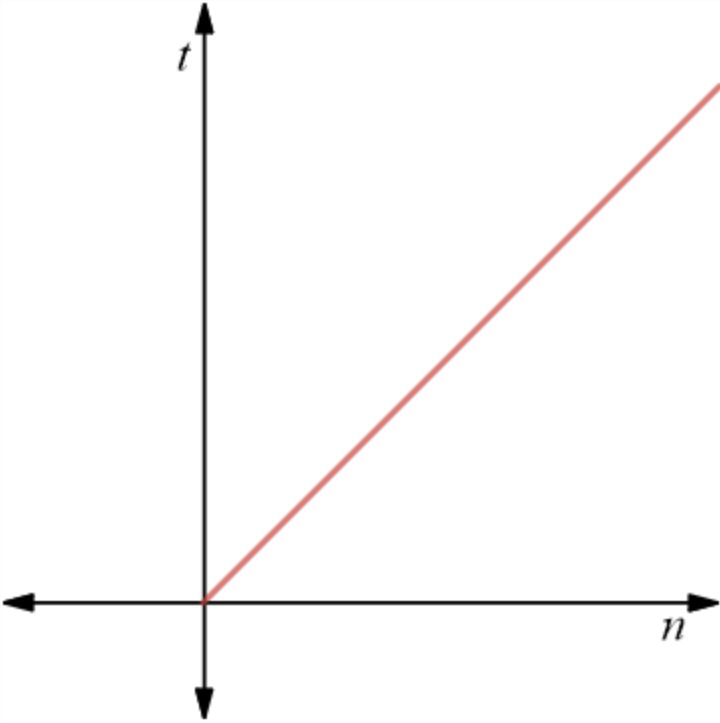
Stabilité
Cette méthode de tri est stable, les valeurs rentrent dans les filles dans un certain ordre et en ressortent dans le même ordre.
5. Comparaison des algorithmes de tri simples
| Algorithme | Complexité au pire | Stabilité | Famille* | Remarques |
|---|---|---|---|---|
| Bulles et améliorations | $ O(n^2) $ | oui | Echange | Sait détecter un tableau trié |
| Extraction | $ O(n^2) $ | non | Sélection | Inefficace sur un tableau déja trié (le pire) |
| Insertion | $ O(n^2) $ | oui | Insertion | Intéressant pour insérer des vleurs dans un tableau déjà trié* |
| Base | $ O(n) $ | oui | Distribution | Intéressant pour les petites valeurs (“petit” nombre de chiffres) |
- On peut trier les valeurs au fur et à mesure. Pour les autres, il est nécéssaire de les avoir toutes avant de commencer. En O(n) dans le meilleur cas.