Directory

Ensembles

On travail en mathématique avec différents ensembles de nombres.

Un ensemble est une collection d’éléments. Ces éléments peuvent être de n’importe quelle nature (nombres, points géométriques, droites, fonctions, autres ensembles, jours de la semaine…)

Appartenance

• Un élément $x$ appartenant à un ensemble $A$ se note: $x \in A$
• La négation se note $x \notin A$

Sous-ensemble

C’est un ensemble dont chaque élément est aussi contenu dans un autre ensemble. Si $A$ est un sous-ensemble de $B$, on note $A\subset B$

si jours = ${lundi, mardi, mercredi, jeudi, vendredi, samedi, dimanche}$ et week-end = ${samedi, dimanche}$, alors week–end $\subset$ jours . Par contre, le singleton ${mardi}$ $\not\subset$ week – end .

Ensemble finis

Un ensemble est fini quand on peut compter ses éléments à l’aide d’entiers tous plus petits qu’un entier donné.

Ils peuvent être définis en extension, par la liste de leurs éléments, et décrits comme tels; on place la liste des éléments d’un ensemble entre accolades, par exemple ${1,3,5}$.

La notation d’un ensemble n’est pas unique, un même ensemble peut être noté de en extension de façons différentes **car l’ordre des éléments est sans importance ${1,2} = {2,1}$.

Définition d’un ensemble en comprehension

Explication de la list comprehension en Python !!!

Un ensemble peut être défini en comprehension, c’est à dire qu’on définit par une propriété caractéristique parmi les éléments d’un ensemble donné.

L’ensemble des entiers naturels pairs est clairement défini par comprehension par la propriété “être pair” parmi les entiers naturels. On écrira:

$$\{x \in \pmb{\mathbb{N}}| x\;\text{pairs}\}\text{ ou } \{2x|x \in \pmb{\mathbb{N}}\}$$

Pour décrire l’ensemble des nombres entiers plus grands que 10, on écrira:

$$\{x \in \pmb{\mathbb{N}}|x>10\}$$

Autres notations

On peut utiliser des points de suspension pour des ensembles de cardinalité infinie, ou finie mais non déterminée.

• Ensemble des entiers naturels peut se noter: $\pmb{\mathbb{N}}=\{0,1,2,3,…\}$

Si il est clair que $n$ désigne un entier naturel, $\{1,2,…,n\}$, voir $\{1,…,n\}$ désigne en général l’ensemble des entiers supérieurs ou égaux à $1$ et inférieurs ou égaux à $n$.

• On peut écrire $\pmb{\mathbb{Z}}=\{…,-3,-2,-1,0,1,2,3,…\}$ ou encore $\{-n,-n+1,…,n-1,n\}$

Quand il y a un procédé itératif simple pour engendrer les éléments de l’ensemble, on peut se risquer à des notations comme $\{0,2,4,6,…\}$ pour l’ensemble des entiers naturels paris, etc…

On peut aussi utiliser ces notations pour des ensembles ayants “beaucoup” d’éléments: $\{1,2,…,1000\}$ ou encore $\{3,5,…,21\}$ à la place de $\{3,5,7,9,11,13,15,17,19,21\}$.

Notations spéciales

• $*$ signifie “sans $0$”, par exemple $\pmb{\mathbb{R}^*}$
• $+$ signifie “plus grand que$0$,($0$ compris)”, par exemple $\pmb{\mathbb{R}_+}$
• $-$ signifie “plus petit que$0$,($0$ compris)”, par exemple $\pmb{\mathbb{R}_-}$

On peut aussi combiner ces symboles: $\pmb{\mathbb{R}^*_+}$

Types de nombres

Entiers naturels $\pmb{\mathbb{N}}$

Les nombres les plus familiers sont les entiers naturels: $0,1,2,3,…$ éléments de l’ensembre $\pmb{\mathbb{N}}$, et utilisés pour le dénombrement.

$\pmb{\mathbb{N}} = \\{0,1,2,3,...\\}$ $\pmb{\mathbb{N}}^* = \pmb{\mathbb{N} \setminus \{0\} = \{1,2,3,...\}}$

Entiers relatifs $\pmb{\mathbb{Z}}$

Si les entiers négatifs sont inclus, on obtient l’ensemble des nombres entiers relatifs $\pmb{\mathbb{Z}}$.

$\pmb{\mathbb{Z}} = \\{...,-3,-2,-1,0,1,2,3,...\\}$ $\pmb{\mathbb{Z}}^* = \pmb{\mathbb{Z}}\setminus \\{0\\}$ Les éléments de $\pmb{\mathbb{Z}}$ correspondent aux graduations d’une droite graduée toutes les unités.

Rationnels $\pmb{\mathbb{Q}}$

La division d’un entier relatif par un entier relatif non nul forme un nombre rationnel. L’ensemble de tous les nombres rationnels est noté $\pmb{\mathbb{Q}}$.

$\pmb{\mathbb{Q}} = \\{\frac{a}{b} | a \in \pmb{\mathbb{Z}}, b \in \pmb{\mathbb{Z}}^*\\}$ Un nombre rationnel est le quotient $a/b$ d’un entier relatif $a$ par un entier naturel non nul $b$. Les nombres rationnels sont ceux qui ont une écriture décimale periodique.

Réels $\pmb{\mathbb{R}}$

Si, dans l’ensemble, outre les éléments de $\pmb{\mathbb{Q}}$, on inclut tous les développements décimaux infinis et non périodiques, on obtient l’ensenble des nombres réels, noté $\pmb{\mathbb{R}}$.

$$\pmb{\mathbb{R}}=\pmb{\mathbb{Q}}\cup\\{...,\pi,e,\sqrt[2]{2},...\\}$$

Tous les nombres réels qui ne sont pas rationnels sont appelés nombres irrationnels.

$\{…,\pi,e,\sqrt[]{2},…\} =$ irrationnels: Les nombres qui ne peuvent pas être mis sous forme de fraction

C’est l’ensemble de tous les nombres usuels. Les réels correspondent aux abscisses possibles d’un point sur une droite graduée. Les nombres réels qui ne sont pas rationnels sont appelés irrationnels. Parmi eux, on trouve $\pi$ ou $\sqrt{2}$.

Ensemble vide $\emptyset$

Cet ensemble est inclus dans tous les autres ensembles

Relations

Nous avons donc une hiérarchie d’ensembles:

$$\emptyset \subset \pmb{\mathbb{N}}\subset \pmb{\mathbb{Z}} \subset \pmb{\mathbb{Q}} \subset \pmb{\mathbb{R}}$$

Ces différents ensembles de nombres sont inclus les uns dans les autres suivant le schéma suivant :

Opérations sur les ensembles

Soit $A$ et $B$ deux sous-ensembles d’un ensemble $E$.

• $E$ est une classe
• $A$ est l’ensemble des filles
• $B$ l’ensemble des élèves portant des lunettes

• Union ( $\cup$ ) correspond à “ou” (fille ou avec lunettes): $A \cup B = \{e \in E | e \in A \text{ ou } e \in B\}$

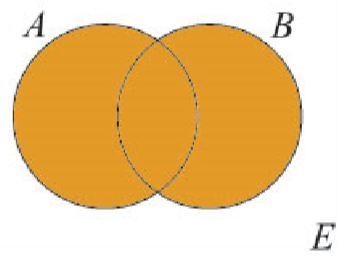
• intersection ( $\cap$ ) correspond à “et” (pour remplire la condition, “ceci” doit être respecté et “celà” aussi): $A\cap B=\{e\in E | e\in A \text{ et }e \in B\}$

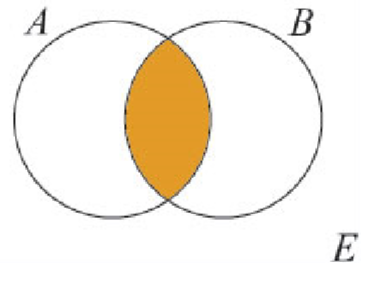
• complémentaire ($C_{Ensemble}$) correspond à “non” (non fille): $C_E A = \{e \in E | e \notin A\}$

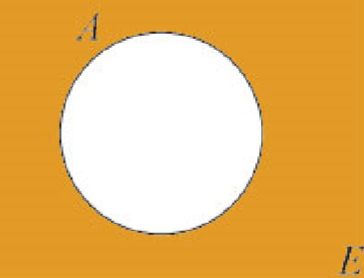
Quand il n’y a pas d’équivique possible, on écrit aussi $\bar{A}$.

• différence ( $\setminus$ ) correspond à “moins” (filles moins avec lunettes) $A \setminus B = \{e \in E | e\in A \text{ et } e \notin B\}$

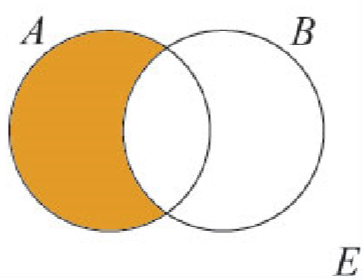
• différencesymétrique (correspond à ou exclusif: ceci ou celà mais pas les deux) $A\Delta B=\{e\in E | e\in A \text{ou (exclusif) } e\in B\}$

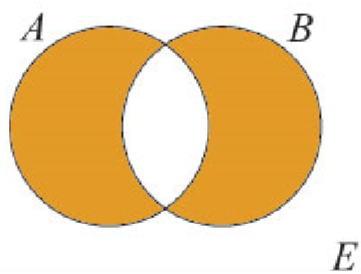
• produit cartésien ( $\times$ ): $A \times B = \{(x;y) | x \in A \text{ et } y \in B\} = \{(x, y) | x \in A, y \in B \}$

C’est à dire l’ensemble de tous les couples possible obtenu en prenant un élément dand $A$ suivi d’un élément dans $B$, dans cet ordre.

$\Rightarrow$ donc $\color{red}{A \times B \neq B \times A}$ !

Exemple: Soit les ensembles $A = \{1, 2\}$ et $B = \{a, b, c\}$

$C = A \times B = \{1a, 1b, 1c, 2a, 2b, 2c\}$

Plan cartésien Le produit cartésien de $\pmb{\mathbb{R}}$ par $\pmb{\mathbb{R}}$ est noté $\pmb{\mathbb{R}}^2 = \pmb{\mathbb{R}} \times \pmb{\mathbb{R}}$ (tous les couples de 2 nombres réels). Il est alors mis en relation avec un plan.

Intervales

Dans $\pmb{\mathbb{R}}$:

$$\begin{align} & x \in [a,b] \color{blue}{\text{ si }} a \le x \le b \color{blue}{\text{ intervalle } \color{red}{ \text{fermé}}} \\ & x \in [a,b[ \color{blue}{\text{ si }} a \le x < b \color{blue}{\text{ intervalle } \color{red}{ \text{ouvert à droite}}} \\ & x \in ]a,b[ \color{blue}{\text{ si }} a < x < b \color{blue}{\text{ intervalle } \color{red}{ \text{ouvert}}} \\ \end{align}$$

Comme $+ \infty$ et $-\infty$ n’appartiennent pas à $\pmb{\mathbb{R}}$ on notera $\pmb{\mathbb{R}} = ]-\infty, +\infty[$

Fractions

Notation décimale vers la notation fractionnaire

Nombres rationnels

Un nombre rationnel est un nombre réel exprimable par le quotient de deux entiers relatifs (appartenant à $\pmb{\mathbb{Z}}$), avec le dénominateur non nul.

Le développement décimal des nombres rationnels a la particularité d’être périodique,c’est à dire qu’il existe un suffixe constitué d’une séquence finie de chiffres se répétant continuellement. Cette séquence est appelée “période du développement décimal illimité”.

Par convention, on trace une barre horizontale au-dessus de la séquence périodique.

Exemples: $\begin{align} & \frac{1}{3} =0.333333…= 0.\overline{3} & \frac{2}{37} =0.054054…= 0.\overline{054} & \frac{115}{74} =1.5540540…= 0.5\overline{540} \end{align}$

Pour trouver la fraction correspondant à un nombre rationnel, il faut soustraire deux multiples de ce nombre de telle façon a ce que la période disparaisse.

Exemple 1: $0.222…=\frac{?}{?}$

Posons $n = 0.222…$

Prenons $10n=2.222…$

On a donc $10n-n=9n$, mais aussi, $2.222…-0.222…=2$.

Donc $9n=2$, ce qui veut dire que $n=\frac{2}{9}$.

Exemple 2: $1.7954\overline{54} = \frac{?}{?}$

$n = 1.7954\overline{54} \Rightarrow 10\;000n=17\;954.\overline{54}$ et $100n = 179,\overline{54}$

$10\;000n-100n = 9900n = 17\;775$

$\Rightarrow n = \frac{17\;775}{9900}=\frac{79}{44}$

Exemple aha: $0,\bar{9}=\frac{?}{?}$

$n=0,\bar{9} \Rightarrow 10n=9,\bar{9}$

$10n - n = 9n = 9,\bar{9}-0,\bar{9}=9$

$\Rightarrow 0,\bar{9} = \frac{9}{9}=1$

Nombres irrationnels

Certains nombres réels ne peuvent pas s’écrire comme quotient de deux entiers. Ces nombres sont dits irrationnels et leur écriture décimale ne contient pas de période. Par exemple $\pi$ et $\sqrt{2}$.

---

Notes pour plus tard

$\Delta = delta = disciminant$