Calcule littéral

L’utilisation des lettres comme notation puis comme objet de calculs, l’enchainement des opérations élémentaires sur des expressions littérales constituent le calcul littéral. Calcul obéit à des règles analogues à celles du calcul numérique.

Puissances

La puissance $n^{ieme}$ d’un nombre réel $a$ est un produit de $n$ facteurs tous égaux à $a$: $a^2 = a \cdot a, \quad a^3 = a \cdot a \cdot a, \quad etc…$

On dit que $a$ est la base de la puissance et $n$ l’exposant: $base^{exposant}$

Pour tous les réels $a$ et $b$ non nuls et tous les entiers $n$ et $m$ non nuls, on a les propriétés suivantes:

$a^n \cdot a^m = a^{n+m}$
$\frac{a^n}{a^m}=a^{n-m}$
$(a^n)^m=a^{n \cdot m}$
$a^n \cdot b^n = (ab)n$
$\frac{a^n}{b^n}=(\frac{a}{b})^n$
$a^{-n}=\frac{1}{a^n}$

Monômes

Un monôme est une expression obtenue par multiplication de nombres et de lettres.

Exemples:

$\frac{1}{3}ab^2\;, \quad -3(xy)^2z\;, ...$

Un monôme est sous forme réduite si l’on effectue le produit des nombres et regroupe les puissances d’une même lettre. Par convention on écrit d’abord le signe, puis le nombre, puis les lettre que l’on place par ordre alphabétique:

$ab\cdot xay (-b) b=-4a^2b^3xy$

Dans un monôme donné sous forme réduite:

Le coefficient du monôme est le nombre (avec le signe)
La partie littérale du monôme est le reste de l’expression et est formé d’une ou plusieurs variables élevées à des puissances entières positives.

Deux monômes sont semblables si après réduction, leur parites littérales sont égales.

Par exemple:

$\frac{1}{3}ab^2 \text{ et } -71ab^2 \text{ sont semblables.}$

Opérations sur les monômes

Multiplication:

$(2ab^2)(3a^4c)=6a^5b^2c$

Élévation à une puissance:

$(2ab^2)^3=8a^3b^6$

Division:

Le résultat n’est en général pas un monôme. Il se peut qu’une des variables du résultat réduit soit élevée à une puissance négative. Il faut préciser les conditions de validité de l’écriture en écartant toutes les valeurs des variables qui annulent le dénominateur (division par 0!).

Exemple: $\frac{3ab^2}{7a^2b} = \frac{3b}{7a}=\frac{3}{7}a^{-1}b\quad(a \neq 0,\; b\neq 0)$

Polynômes

Un polynôme est une somme ou une différence de monômes.

Le degré d’un polynôme par rapport à une lettre est la plus grande puissance à laquelle cette lettre est élevée dans le polynôme.

Exemple: $\text{le polynôme }\frac{1}{3}ax^4 - 3bx +2 \text{ est de degré 4 pour la lettre } x$

Un polynôme est sous forme réduite si chaque monôme composant celui-ci est réduit et si l’on a regroupé tous les monômes semblables.

Opérations sur les polynômes

On regroupe, additionne ou soustrait tous les monôme semblables. Le résulatat est donné sous forme réduite.

On utilise les expressions suivantes de façon équivalentes:

effectuer le produit de polynômes
distribuer et réduire
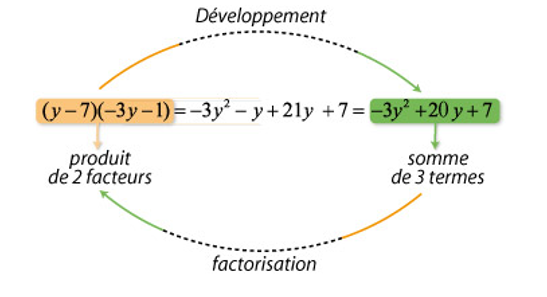
développer

Ces opérations consistent toutes à transformer une expression algébrique donnée sous la forme d’un produit de termes en une somme de termes.

Exemple:

$\begin{align} (7x^2-3x+4)(x-3) & = 21x^2-3x^2+9x+4x-12 \\ & = 7x^3-24x^2+13x-12 \\ \end{align}$

Rappel:

$(x+3)(x^2-1)(2x+1)=(x^3-x+3x^2-3)(2x+1) = ...$

Factorisation

Factoriser consiste à transformer une somme de termes en un produit de facteurs.

Tout polynôme $P(x) \in \pmb{\mathbb{R}}[x]$ est un produit de polynômes du premier degré et du second degré à discriminant ($\Delta=b^2-4ac$) négatif (pas de racines).
Si $P(x) \in \pmb{\mathbb{Z}}[x]$ est un polynôme à coefficient entiers, alors ses seules racines entières possibles sont les diviseurs de $P(0)$, c’est à dire les diviseurs du terme constant.
Si $P(x) \in \pmb{\mathbb{R}[x]}$ admet $c$ comme racine, alors il est divisible par $d(x)=x-c$

Produits remarquables

$(a+b)^2 = a^2+2ab+b^2$
$(a-b)^2 = a^2-2ab+b^2$
$(a+b)(a-b) = a^2-b^2$
$(a+b)^3=a^3+3a^2b+3ab^2+b^3$
$(a-b)^3=a^3-3a^2b+3ab^2+b^3 $
$(a+b)(a^2-ab+b^2)=a^3+b^3$
$(a-b)(a^2-ab+b^2)=a^3-b^3 $

Toutes ces formules se démontrent en développant le terme de gauche.

Mise en évidence

On met en évidence les symboles apparaissant dans plusieurs termes d’une expression.

Factorisation par tatonnement

Pour factoriser un polynôme de second degré, il faut trouver (par tatonnement) deux nombres $a$ et $b$ dont la somme correspond au deuxième terme et le produit au troisième terme. Il est plus facile de commencer le tatonnement par le produit.

Exemple:

$x^2 + 11x +28 = (x+4)(x+7)$

On tatonne ainsi:

$28 = 1 \cdot 28 \text{ mais }1+28 \neq 11$

$28 = 2 \cdot 14 \text{ mais }2+14 \neq 11$

$28 = 4 \cdot 7 \text{ et }4+7 = 11$

Factorisation par groupement

Lorsque l’on a un nombre pari de termes, on peut essayer de factoriser par groupement:

$\begin{align} 64x^3-16x^2-100x+25 & = \bbox[5px,border:1px solid blue] {64x^3-16x^2} \bbox[5px,border:1px solid red] {-100x+25} \\ & = \bbox[5px,border:1px solid blue] {16x^2(4x-1)} \bbox[5px,border:1px solid red] {-25(4x-1)} \\ & = (16x^2 -25)(4x-1) \\ & = (4x + 5)(4x-5)(4x-1) \end{align}$

Technique de Viett (discriminant ($\Delta$))

$P(x) = ax^2 + bx + c $

$\begin{align} \Delta & = b^2 - 4ac \\ \text{si} \Delta \ge 0 & \Rightarrow x_{1,2} = \frac{-b \color{blue}{\pm} \sqrt{\Delta}}{2a} \Rightarrow p(x) = \color{red}{a} (x - x_1)(x-x_2) \\ \text{si} \Delta < 0 &\Rightarrow \text{pas de racines.} \end{align}$

Division de polynômes

On appelle racine d’un polynôme la valeur $x = r$ telle que $P(r) = 0$
Si $r$ est une racine, $P(x)$ est alors divisible par $(x-r)$ et le reste est nul.
Si $r$ n’est pas une racine, alors le reste n’est pas nul et la valeur numérique du reste est égale à $P(r)$.
Un polynôme de degré $n$ peut avoir jusqu’à $n$ racines réelles. Un polynôme de degré impaire a toujours au moins une racine réelle.

Un polynôme de degré $n$ a $n$ racines, mais certaines peuvent être des nombres complexes.

Exemple: Soit $P(x) = x^4 -2x^3 - 7x^2 +8x +12$. Ce polynome est de degré 4, il y a donc 4 racines réelles au maximum. Divisons $P(x)$ par $(x-3)$:

$\begin{array}{ccccc|ccc} x^4 & -2x^3 & -7x^2 & +8x & +12 && (x&-&3) \\ \hline -x^4 & -3x^3 &&&& x^3 \\ & -x^3 \\ & -x^3 & -3x^2 &&&& +x^2 \\ && -4x^2 \\ && -4x^2 & +12x &&&& -4x \\ &&& -4x \\ &&& -4x & +12 &&&& -4 \\ &&& 0 & 0 \\ \end{array}$

$P(x)$ peut alors se factoriser: $(x-3)(x^3+x^2-4x-4)$ Esseyons maintenant de diviser $P(x)$ par $(x-1)$

$\begin{array}{ccccc|ccc} x^4 & -2x^3 & -7x^2 & +8x & +12 && (x&-&1) \\ \hline x^4 & -x^3 &&&& x^3 \\ & -x^3 \\ & -x^3 & -x^2 &&&& -x^2 \\ && -8x^2 \\ && -8x^2 & +8x &&&& -8x \\ && 0 & 0 \\ &&&& \color{red}{R: 12}\\ \end{array}$

On voit que $P(x)$ n’est pas divisible par $(x-1)$, car le reste vaut 12. 1 N’est donc pas une racine. D’autre part, on remarque que $P(1) = 12$

Valeur absolue

$|f(x)| = a \Rightarrow f(x) = -a \text{ ou } f(x)= a$

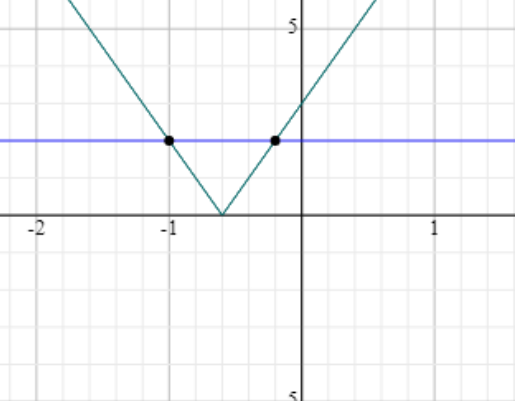
Exemple1:

$|5x+3|=-2$

$5x+3=2 \Rightarrow x = -\frac{1}{5}$
$5x+3=-2 \Rightarrow x = -1$

POUR PLUS TARD

Ne jamais diviser par l’inconnue. $\Rightarrow$ perte de solutions.

Directory