Rappel: vecteurs du plan euclidien

Un vecteur est complètement caractérisé lorsque l’on connait la longueur, la direction et le sens de la flèche qui le représente.

Opérations sur les vecteurs:

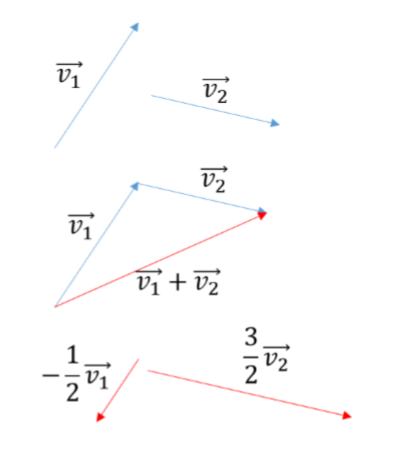
Somme de deux vecteurs $\vec{v}_1$ et $\vec{v}_2$: La fléche représentant $\vec{v}_1 + \vec{v}_2$ s’obtient en mettant bout à bout les deux fleches représentant $\vec{v}_1$ et $\vec{v}_2$.
Multiplication d’un vecteur $\vec{v}$ par un nombre réel $\lambda$: La fleche représentant $\lambda \vec{v}$ a la direction de $\vec{v}$; sa longueur vaut $\lambda$ fois celle de $\vec{v}$ et son sens est celui de $\vec{v}$ (contraire à $\vec{v}$) si $\lambda > 0$ ($\lambda < 0$).

Dans le plan euclidien $\pmb{\mathbb{R}}^2$, considérons une base orthonormée (un ensemble de deux vecteurs $\vec{u}_x$, et $\vec{u}_y$ unitaires 9de longueur unité chacun) et perpendiculaires entre eux. Appelons $x$ et $y$ les axess que supportent $\vec{u}_x$, et $\vec{u}_y$ respectivement.

Tout vecteur $\vec{c} \in \pmb{\mathbb{R}}^2$ s’écrit de manière unique: $\vec{v}=v_x\cdot \vec{u}_x + v_y \cdot \vec{u}_y$ Où $v_x$ et $v_y$ sont des nombres réels appelés composantes $x$ et $y$, respectivement, de $\vec{v}$. De manière equivalente, on peut écrire:

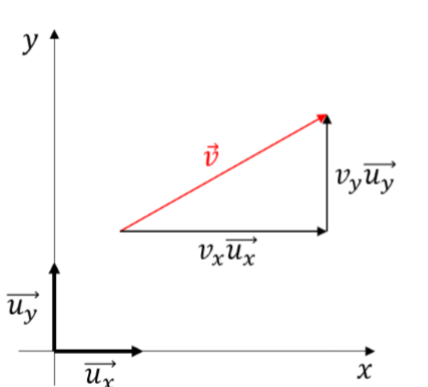
$\vec{v} = \begin{pmatrix} v_x \\ v_y \\ \end{pmatrix}$

Un vecteur $\vec{v}$ est complètement carctérisé par la donnée de ses composantes $v_x$ et $v_y$ par rapport à une base de $\pmb{\mathbb{R}}^2$.

Opérations sur les vecteurs, donnés en composantes:

$\vec{v} = \begin{pmatrix} v_x \\ v_y \\ \end{pmatrix}, \vec{w} = \begin{pmatrix} w_x \\ w_y \\ \end{pmatrix}$

Somme de deux vecteurs:

$\vec{v}+ \vec{w}=\begin{pmatrix} v_x \\ v_y \\ \end{pmatrix} + \begin{pmatrix} w_x \\ w_y \\ \end{pmatrix} = \begin{pmatrix} v_x + w_x \\ v_y + w_y \\ \end{pmatrix}$

Multiplication par un nombre réel $\lambda$:

$\lambda \vec{v} = \begin{pmatrix} v_x \\ v_y \\ \end{pmatrix} = \begin{pmatrix} \lambda v_x \\ \lambda v_y \\ \end{pmatrix}$

Normes (longueur ou intensité) d’un vecteur $\vec{v}$

$||\vec{v}|| = v = \sqrt[]{v_x^2 + v_y^2}$

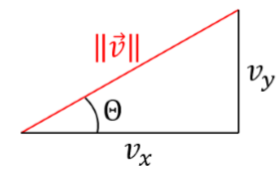
Si $\theta$ est l’angle entre $\vec{v}$ et l’axe $x$ alors:

$\vec{v}=\begin{pmatrix} v_x \\ v_y \\ \end{pmatrix} = \begin{pmatrix} ||\vec{v}|| \cdot cos\; \theta \\ ||\vec{v}|| \cdot sin\; \theta \\ \end{pmatrix} = ||\vec{v}||\begin{pmatrix} cos\; \theta \\ sin\; \theta \\ \end{pmatrix} = ||\vec{v}|| \cdot \vec{u}$

Où \vect{u} est un vecteur unitaire ayant la direction (et le sens) de $\vec{v}$.

Application à la force de Coulomb

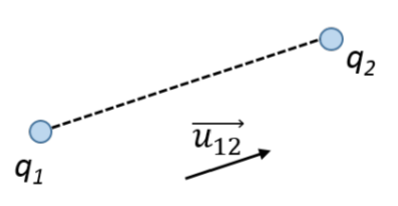
Soit deux charges $q_1$ et $q_2$ et $\vec{F}_{AB}$ la force exercée sur $A$ par $B$:

$\vec{F}{12} = +F\cdot \vec{u}{12} = - \vec{F}_{21}$ (si $q_1$ et $q_2$ sont de signe opposé)
$\vec{F}{12} = -F\cdot \vec{u}{12} = - \vec{F}_{21}$ (si $q_1$ et $q_2$ sont de même signe)

Où $F = \frac{1}{4 \pi \epsilon_0} \frac{|q_1\;q_2|}{d^2}$ et $\vec{u}_{12}$ un vecteur unitaire selon le segment $q_1\; q_2$

Principe de superposition

Soit $n$ charges (ponctuelles) $1_1,q_2,…q_n$. Pour trouver la force électrique totale que ces $n$ charges produisent sur une charge $Q$ donnée, on applique le principe suivant:

La force entre deux charges ne dépend pas des aurtes charges en présences.
La force résultante sur $q_0$ est la somme vectorielle des forces exercées par chacune des $n$ charges $q_1,…,q_n$ sur $q_0$, calculées l’une après l’autre:

$\vec{F}_0^{tot} = \vec{F}_{01} + \vec{F}_{02} + ... + \vec{F}_{0n}$

Où $\vec{F}_{0i}$ est la force exercée sur $q_0$ par la i-ème charge, $q_i$